- Введение. Моделирование и изучение нейронных сетей представляется сейчас одним из приоритетных научных направлений. При этом до сих пор имеется определенный дефицит моделей нейронного элемента, с одной стороны, достаточно простых, а с другой стороны, потенциально способных порождать нейронные сети со сложным поведением. Важно также иметь возможность изучать полученные нейронные сети как аналитическими, так и численными методами.
На пути построения такой модели была предложена математическая модель обобщенного нейронного элемента (ОНЭ) [1]. Для ОНЭ-сетей были получены перспективные аналитические результаты (например, [2], [3]). Затем в [4] была введена имитационная модель модифицированной сети обобщенных нейронных элементов, которая позволила упростить формальное описание нейронной сети в целом. В настоящей статье приводится алгоритм реализации модифицированных ОНЭ-сетей на ЭВМ. Это позволит провести численные исследования больших сетей со сложной архитектурой.
- Модифицированная сеть обобщенных нейронных элементов. Рассмотрим нейронную сеть, состоящую из N элементов, которая функционирует в непрерывном времени t. Сеть определяется следующим набором параметров:

Поведение произвольного k-го элемента сети определяется двумя функциями, зависящими от времени t:




- Алгоритм реализации МОНЭ-сетей на ЭВМ. Наиболее естественным способом программной реализации нейронной сети является разработка параллельного алгоритма. В соответствии с такими алгоритмами происходит функционирование нейрокомпьютеров. Но для стандартных вычислительных систем использование параллельных алгоритмов, в соответствии с которыми нейроны на самом деле функционируют одновременно, затруднительно.
Рассмотрим последовательную алгоритмическую реализацию МОНЭ-сетей. Для удобства реализации на ЭВМ некоторые параметры модели очевидным образом преобразованы в допустимые для программирования символы. Также в целях экономии памяти и повышения быстродействия перейдем к одномерным массивам.
Для каждого из N элементов обозначим (и будем хранить в подходящих типах данных) следующие статические параметры:
- n_i – число входов данного элемента;
- m_i – число выходов данного элемента;
- num_in_i – одномерный массив длиной n_i с номерами элементов, имеющих связь по направлению к данному элементу;
- num_out_i – одномерный массив длиной m_i с номерами элементов, имеющих связь по направлению от данного элемента;
- q_i – одномерный массив длиной n_i с весами связей, ведущих к данному элементу.
Для каждого из N элементов обозначим (и будем хранить в подходящих типах данных) следующие динамические параметры:
- s_i – текущее состояние (1 – восприимчивость, -1 – рефрактерность);
- u_i – текущая величина мембранного потенциала;
- t_event_i – время до события;
- sigma_i – одномерный массив длиной n_i индикаторов связей,
ведущих к данному элементу.
Все эти параметры различны у разных элементов сети, задаются пользователем в начальный момент времени, а в дальнейшем меняются.
Другие важные характеристики сети и соответствующие им переменные:
- t – текущий момент времени;
- delta – временной промежуток до ближайшего события в сети;
- type_event – тип события (1, если p-событие, -1, если 0-событие);
- num – номер элемента, с которым происходит событие.
Алгоритм включает в себя следующие стадии.
- Задание пользователем параметров N, p, r, alpha и T_ R.
- Программная отрисовка конкретной МОНЭ-сети или задание пользователем ее топологии в интерактивном режиме с указанием весов связей. При этом для каждого элемента определяются все статические параметры.
III. Задание начального состояния сети в соответствии с введенной моделью. При этом для каждого элемента определяются все динамические параметры. Если для i-го элемента s_i=-1 (рефрактерность), то нужно задать и время t_event_i, в данном случае до выхода из рефрактерности. Если s_i=1 (восприимчивость), то время t_event_i, в данном случае до генерации импульса, задавать не нужно. Оно функционально определяется остальными параметрами данного нейрона:
 (3)
(3)
где sum_i – сумма чисел q_i[j] по всем таким j=1,2,…,n_ i, что sigma_i[j]>0. Массив sigma_i инициализируется нулями. После задания начального состояния сеть готова к функционированию.
- В первом цикле по всем элементам сети вызывается функция, которая обновляет величину t_event_i для каждого i-го элемента по формуле (3), если s_i=1.
Во втором цикле по всем элементам сети определяется величина delta:
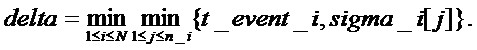
При расчете величины delta берутся только положительные элементы sigma_i[j] (иначе величина delta всякий раз будет равна нулю). В этом же цикле находятся величины type_event и num. Все найденные величины записываются в соответствующие переменные.
- Зная тип события type_event, номер элемента num и время delta, переходим к пересчету всей сети. В зависимости от типа события это происходит по-разному.
В любом случае сначала для всех, кроме num-го, элементов сети, для которых s_i=1, обновляются величины мембранных потенциалов u_ i по формуле:

Наконец, в любом случае для всех элементов сети, кроме num-го, все величины t_event_i уменьшаются на величину delta.
- Для наглядного представления динамики сети на экране имитируется визуальная пауза (пропорциональная величине delta), а затем происходит отрисовка произошедшего события.
На этом переход сети от состояния, соответствующего моменту времени t, к состоянию, соответствующему моменту времени t+delta, закончен. Поэтому переменная delta обнуляется, а общее время функционирования сети t пересчитывается: ![]()
Далее происходит переход к шагу IV, и шаги IV – VI повторяются циклически до тех пор, пока пользователь не остановит функционирование МОНЭ-сети. Изложение алгоритма закончено.
Данный алгоритм способен работать сколь угодно долго, и с помощью него можно получить состояние сети в любой момент времени. Кроме того, алгоритм устроен так, что он легко может осуществляться и по шагам, и непрерывным образом. Пошаговое выполнение удобно для контроля над характеристиками сети в конкретный момент времени. Возможность такого контроля (наблюдения за такими характеристиками, но не изменения их) должна быть предоставлена пользователю. К важнейшим таким характеристикам относятся: величины мембранных потенциалов, последовательные рассогласования между импульсами одного и того же элемента, последовательные рассогласования между импульсами соседних элементов. Согласно гипотезе фазово-частотного кодирования информации мозгом, именно величины таких рассогласований в устойчивых колебательных режимах нейронной активности являются информационным носителем [5]-[7].
Список литературы:
- Майоров В.В., Коновалов Е.В. Обобщенный нейронный автомат в задаче распространения волны возбуждения по нейронной сети // Нейрокомпьютеры: Разработка, применение. М.: Радиотехника, 2007. № 7. – С. 3-8.
- Коновалов Е.В. Устойчивый колебательный режим в нейронной сети обобщенных нейронных автоматов-детекторов // Моделирование и анализ информационных систем. Ярославль: ЯрГУ, 2007. Т.14, № 2. – С. 30-35.
- Коновалов Е.В. Задача адаптации обобщенного нейронного элемента // Моделирование и анализ информационных систем. Ярославль: ЯрГУ, 2012. Т.19, № 1. – С. 69-83.
- Коновалов Е.В. Модифицированная сеть обобщенных нейронных элементов. Междисциплинарные исследования в области математического моделирования и информатики: Материалы 4-й научно-практической internet-конференции. Ульяновск, SIMJET. – 2014. – С. 88-93.
- Бехтерева Н. П. Нейрофизиологические аспекты психической деятельности человека. Л: Медицина, 1971. – 120 с.
- Ливанов М. Н. Торможение в нейронных системах коры головного мозга. Рефлексы головного мозга: Сборник трудов Международной конференции, посвященной 100-летию со дня выхода в свет книги И.М. Сеченова «Рефлексы головного мозга» М.: Наука, 1965. – С. 64-71.
- Лебедев А. Н. Память человека, ее механизмы и границы (в сб. Исследование памяти под ред. Н. Н. Коржа). М.: Н[schema type=»book» name=»АЛГОРИТМ РЕАЛИЗАЦИИ МОДИФИЦИРОВАННЫХ СЕТЕЙ ОБОБЩЕННЫХ НЕЙРОННЫХ ЭЛЕМЕНТОВ НА ЭВМ » description=»В статье рассматривается модель модифицированной сети обобщенных нейронных элементов и приводится алгоритм реализации модифицированных сетей обобщенных нейронных элементов на ЭВМ.» author=»Коновалов Евгений Владиславович» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-02-20″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_25.07.15_07(16)» ebook=»yes» ]

