Геодинамические процессы внутри Земли, на ее поверхности и в прилегающих слоях атмосферы могут изучаться не только за счет лишь движения масс вещества. Если рассматривать состояния подобных опасных явлений, то становится возможным исследовать их на фоне динамики устойчивостей нелинейных систем. Природные катастрофические опасности (наводнения, землетрясения, засухи, ураганы, смерчи и т.п.) вызываются действием стихийных сил природы. Человеческое общество пока не в состоянии их полностью предотвратить. Но своей деятельностью, например, по их предсказанию — научному прогнозу, оно может минимизировать потери, и напротив, своей бездеятельностью или необдуманными действиями (уничтожение лесов, источников воды, загрязнение среды обитания и т.п.) может многократно усилить имеющийся у природы разрушительный потенциал. Экологические катастрофические опасности вызываются локальными или планетарными дисфункциями биосферы. Растущее давление человека на природу подрывает восстановительную способность биосферы, ее основных звеньев и, в конечном счете, вызывая локальные катастрофические опасности, готовят условия для катастрофической опасности глобальной.
Эффективность систем управления риском и ликвидацией последствии чрезвычайных событий (ЧС) природного и техногенного характера может быть повышена путем разработки математических и алгоритмических средств, адекватных сложности поставленной проблемы. Перспективным направлением исследований по данной проблеме является разработка научно-методических основ сценарного подхода и прикладных методов создания и развития систем.
Сценарии развития сложной региональной системы принадлежат к классу так называемых неполных математических моделей, т.е. моделей, в которые включены лишь те существенные факторы или интегральные характеристики, которые могут быть формализованы с приемлемой степенью точности. Например, в работах [2,3] предложено принять изменения численности населения за интегральную характеристику устойчивого развития региона. В результате проведен временной анализ устойчивого развития Кировско – Апатитского района Мурманской области, и сделан вывод, что, начиная с 1990 по настоящее время, имеется неустойчивое развитие региона.
Несмотря на то, что за последние десятки было потрачено триллионы долл., экологическая обстановка на Земле ухудшается. В глобальной экономике развиваются две противоположные тенденции: глобальный валовой доход растёт, а глобальное богатство (прежде всего жизнеобеспечивающие ресурсы) уменьшается.
Деградация природной среды прямым образом влияет на активизацию опасных природных процессов с тяжёлыми экологическими последствиями, возросло за последние пятилетия более чем несколько раз.
Понятие «катастрофа» значительно шире и относится вообще ко всякому конечному результату столкновения противоборствующих устремлений. Философское определение катастрофы сводится к разрушению единства, сопровождаемого ожесточенными столкновениями частей между собой, нарастающую дезорганизацию, неспособность предотвратить переход через опасный порог. Являясь конечной вершиной действия, катастрофа не является, однако, непосредственно его концом: действие может продолжаться и после катастрофы, но уже в том направлении, которое определено характером противоборствующих устремлений.
Теория хаоса, позволяющая описывать адаптационные и бифуркационные механизмы развития систем, определяет катастрофу как переход системы в иное состояние (изменение структуры). Прежнее состояние системы разрушается в результате флуктуации, которая не играет особой роли в развитии системы до тех пор, пока не достигает области неустойчивости, присущей любой системе. В этой теории катастрофа рассматривается как этап эволюции системы, а тем самым подчеркивается значимость катастроф для развития любой системы.
Время появления значимых подобных событий в пределах сотни лет можно считать случайным. Амплитуды опасностей в большинстве случаев не поддаются предсказанию, т. е. величина их также случайна. Эти общие свойства позволяют характеризовать состояние опасности как переменную отношений в реляционном подходе метафизики. В свою очередь для географии природных опасностей важно, что переменные математической структуры, построенной аксиоматически, не требуют определения природы тех элементов, которые образуют ту или иную структуру.
Процесс нарастания природных опасностей с математической точки зрения описывается экспоненциальной зависимостью, что связано с вовлечением в процесс собственной «массы» опасности. При наличии противоборствующих сил в первом приближении подобные процессы описываются уравнением Ферхюльста. Оно является частным вариантом (Q<0, А=L) общего автономного дифференциального уравнения 2-го порядка для функции x(t) от времени t , т.е.
dx/dt=N+L*x+Q*, (1)
где N,L,Q – константы уравнения с начальными условиями и для n=0,1,2,… Полное решение этого уравнения с произвольными начальными условиями имеет громоздкий вид [1,4], хотя качественно вполне отражается логистической кривой. Однако эти решения позволяют выявить принцип нарушения устойчивости решений численного логистического уравнения

Отметим, что дискретное представление позволяет использовать специальным образом свойства матричного аппарата. Например, в работах [5,6] удачно применяется матричный подход для исследования динамики экосистем с учетом существующих воздействий, а также осуществляется матричный прогноз и сделаны приближенные расчеты о том, какое управление человеком необходимо, чтобы соблюдалась гармония между человеком и окружающей средой.
Показано, что неустойчивость процессов с противоборствующими факторами вызывается перепадами исходных условий на последовательных отрезках. При определенных значениях параметров дифференциального уравнения, связанных с емкостью напряженной среды, могут формироваться как неустойчивые, так и детерминированные режимы развития переменной x(t), нормированной на единицу. Отмечен пример в качестве модели Ферхюльста с параметром А, для которой на рис.1 приведены зависимости решений x(t) в интервалах времени и табличных значений x(n)= , а также показаны с различными а=А* перепады начальных условий.
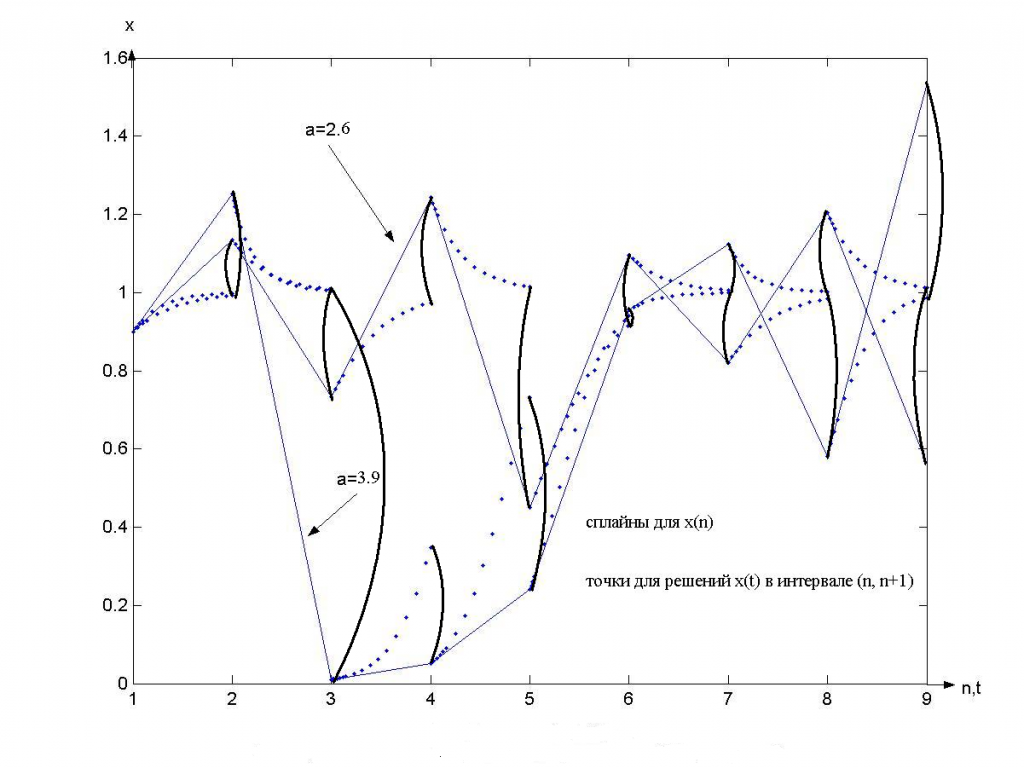
Рисунок 1. Зависимость решений x(t) в интервалах и табличных значений x(n)= . Дугами “(“ при a=2.6 и “)” при a=3.9 показаны перепады начальных условий.
На рис. 1 присутствуют отрицательные наклоны у зависимости, связанной с табличными . Отсюда появляется ситуация, которая приводит к выходу переменной x из коридора, нормированного на единицу, устойчивых значений.
Таким образом, динамика опасностей, а, именно, катастрофические переходы из одного состояния в другое, вполне могут характеризоваться скачками обобщенной переменной (по типу рис.1) в дискретных точках сложных зависимостей во времени. Следовательно, приведенное численное логистическое уравнение (2) можно принять в первом приближении за числовую модель развития природных опасностей в географической среде, характеризуемой емкостью (параметр a) напряжения противоборствующих факторов.
Список литературы:
- Кудин В.Н. О нарушении устойчивости решений численного логистического уравнения. Сборник научных трудов «Физические проблемы экологии». М. 2008, №15, с. 198-205.
- Светлосанов В.А., Кудин В.Н., Куликов А.Н. О понятиях «устойчивость» и «устойчивое развитие». Журнал: Экологические системы и приборы, 2006. №7. с.11-15.
- Светлосанов В.А., Кудин В.Н., Куликов А.Н. О критериях оценки устойчивого развития региона. Журнал: Юг России: Экология, развитие. 2008, № 1. с.6-14.
- Светлосанов В.А., Куликов А.Н., Кудин В.Н. Логистическая кривая — порядок и хаос в природных системах. Журнал: Экологические системы и приборы, 2009, №7. с.42-46.
- Светлосанов В.А., Кудин В.Н. Системный анализ, риск, порядок и хаос в стратегии устойчивого развития. Журнал: Экологические системы и приборы. 2012. № 11, с. 58-64.
- Светлосанов В.А., Кудин В.Н. Матричный подход при анализе динамики экосистем. Журнал: Экологические системы и приборы, 2012. № 12. с. 30-33.[schema type=»book» name=»Числовая модель развития природных опасностей в напряженной противоборствующими силами среде» description=»Показано, что неустойчивость процессов с противоборствующими факторами вызывается перепадами исходных условий на последовательных отрезках. При определенных значениях параметров дифференциального уравнения, связанных с емкостью напряженной среды, могут формироваться как неустойчивые, так и детерминированные режимы развития. » author=»Кудин Валерий Николаевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-05-30″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_ 30.12.2014_12(09)» ebook=»yes» ]

