Наиболее значимым и наиболее понимаемым моментом субстратного подхода является идея нахождения всегда и везде самого главного момента в выявляемых фрагментах информационного контекста проблемы, которые называются субстратными классами. С этой целью автором совместно с А.А. Гагаевым разработана гносеологическая схема выделения самого главного на пяти уровнях абстрактного мышления [1-5] (табл. 1).
Анализ любой системы с целью ее качественной оптимизации проводится на пяти уровнях абстрактного мышления. Под качественной оптимизацией здесь понимается не традиционная классическая оптимизация целевой функции управления с помощью математической модели, а, так называемая, субстратная оптимизация, которая подразумевает выявление определенных качественных показателей (субстратных классов и субстратов), влияющих на максимизацию или минимизацию целевой функции управления, которая в частных случаях может иметь и количественное описание в виде числового значения параметра оптимизации.
Таблица 1. Гносеологическая схема связи категорий, уровней абстрагирования, способов познания и целевых подсистем, применительно к решению проблемы субстратной оптимизации любых систем, в том числе и систем государственного управления
| Основания | |||||
| классификации |
ЦЕЛЕВЫЕ ПОДСИСТЕМЫ |
||||
| Способ познания | Всеобщее | Общее | Конкретно абстрактное | Особенное | Конкретно- отдельное |
| Уровень абстрагирования | Уровень целостности | Уровень класса задач | Уровень обобщенного алгоритма | Уровень конкретной схемы управления | Уровень практики |
| Номер уровня | 4 | 3 | 2 | 1 | 0 |
| Вид системы | Идеальная | Идеальная | Идеальная | Идеальная | Материальная |
| Концепт системы | Свойство целостности | Свойство общности между задачами управления
(субстрат) |
Отношение связи между блоками | Отношение связи между функциями управления | Свойство зависимости
эффективно- сти управления от методов |
| Структура системы | Отношение соподчиненности между уровнями абстрагирования | Отношение принадлежности к задачам управления | Набор свойств, получаемых при структурном разбиении проблемы | Набор
свойств, описываемых блоками схемы управления |
Отношение между объектами управления |
| Анализируемые системы | Система систем, образующих иерархию | Все задачи управления | Обобщенный алгоритм управления | Схема управления конкретным объектом | Анализируемый объект управления |
Таким образом, субстратная оптимизация в своей основе имеет не математический аппарат, а философский. Именно на этих принципах, как установил автор, основан процесс эволюции животного и растительного мира, в котором выживают те особи, которые лучше других (качественно оптимально) приспособились к процессу выживания в условиях конкурентной борьбы. Уровни абстрагирования обозначаются цифрами от 0 до 4 включительно. Приведем алгоритм движения по уровням абстрагирования с целью качественной оптимизации системы в виде следующей последовательности цифр: 0 – 4 – 3 – 2 – 1 – 0. Этот алгоритм мы назвали всеобщим алгоритмом движения по уровням абстрагирования. Здесь:
0 – уровень практики, материального бытия. На этом уровне формулируются прикладные проблемы, которые мы хотим решить максимально эффективным образом, хотим построить оптимальную стратегию управления и т.д.
4 – наивысший уровень абстрагирования, отражающий всеобщее, предельно главное. Например, при рассмотрении системы самым главным моментом является достижение системного эффекта. В других случаях – это достижение качественной оптимизации стратегии и т.д.
3 – уровень общего. На этом уровне мы выявляем и ранжируем по значимости субстратные классы и в каждом таком классе находим субстраты – ключевые моменты оптимизации целевой функции управления.
2 – уровень конкретно-абстрактного. На этом уровне из выявленных субстратов мы строим качественно оптимальную стратегию управления объектом.
1 – уровень особенного. Диалектика познания здесь проявляется в том, что на предыдущих уровнях 4, 3, 2 мы имели дело с разными степенями общего, которые определяют основные (всеобщие, общие и конкретно-абстрактные моменты качественной оптимизации). Но в некоторых случаях большое значение приобретает специфика объекта или процесса управления. Вот как раз для этого мы и применяем первый уровень абстрагирования, учитывая специфические особенности объекта или процесса управления.
0 – уровень практики. В точном соответствии с известной философской формулировкой «от живого созерцания к абстрактному мышлению и от него к практике, таков диалектический путь познания истины, познания объективной реальности» мы переходим к процессу практического применения полученных нами результатов.
Описанный выше процесс можно более наглядно представить в виде алгоритма достижения системного эффекта (рис. 2) [6-13].
Этот алгоритм имеет итерационный характер. Дело в том, что классы и субстраты являются философскими сущностями, которые как бы не лежат на поверхности. Найти их в конкретных ситуациях управления не так то просто. Кстати, для этого требуется специальный способ мышления, детально описанный Гагаевым А.А. [3]. Для развития и тестирования субстратной рефлексии автором разработана серия уникальных компьютерных моделей, с помощью которых можно демонстрировать все особенности применения субстратного подхода для решения предельно широкого класса прикладных задач в любой сфере человеческой деятельности. Это и понятно. Философия, на базе которой разработан субстратный подход применима везде.
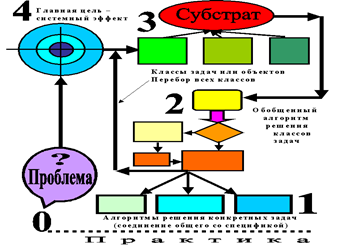
Рис. 2. Алгоритм достижения системного эффекта и субстратной оптимизации систем в виде итерационного процесса. Цифры – это номера уровней абстрагирования
Понимание этого факта – один из моментов высочайшей научной и практической значимости субстратного подхода.
Вторым значимым моментом субстратного подхода является оригинальная трактовка свойства гомоморфизма моделей, которая приводится на рис. 2.
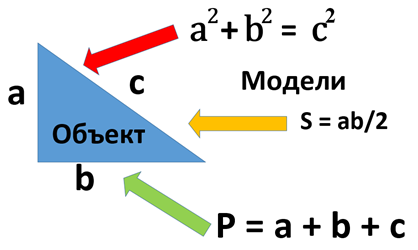
Рис. 3. Объяснение гомоморфизма моделей на примере прямоугольного треугольника
Классическое определение гомоморфизма моделей заключается в том, что свойство гомоморфизма связывают с одно направленностью потока корректной информации от модели к объекту, но ни в коем случае не наоборот. Субстратная трактовка гомоморфизма, которую предлагаем мы, более доступна для понимания. Рассмотрим прямоугольный треугольник в качестве объекта моделирования (рис. 3). Тогда для этого объекта можно построить несколько гомоморфных моделей, каждая из которых будет описывать свой конкретный субстратный класс в моделируемом объекте. Например, теорема Пифагора будет описывать только соотношение длин сторон а, b и с, формула параметра S будет описывать только численную величину его площади, параметр Р будет описывать только сумму длин его сторон и т.д. Такое понимание гомоморфизма открывает колоссальные возможности моделирования при решении прикладных проблем качественной оптимизации объектов и процессов, например, управления.
Покажем это на уникальной гомоморфной модели качественной оптимизации государственного управления Sum. Описанная выше теория субстратного гомоморфизма открывает безграничные возможности моделирования процессов качественной оптимизации любых систем. В качестве примера возьмем процесс предупреждения дефолта организации с помощью качественной оптимизации стратегии управления. Теория гомоморфизма позволяет предельно упростить любую прикладную задачу, отбрасывая несущественные в конкретной ситуации управления аспекты моделирования и делая акцент на тех моментах функционирования объекта, на тех его субстратных классах, от которых в данной ситуации управления зависит конечный результат. Этот прием в моделировании называется декомпозицией проблемы, т.е. строго целенаправленным и научно обоснованным разделением ее на части. В качестве учебного, экспериментального закона функционирования объекта управления возьмем процесс сложения двух девятизначных чисел, первое слагаемое которого описывает внешнюю среду управления, второе слагаемое – внутреннюю среду, а сумма – конечный результат. Количество таких параметров в данном случае несущественно и может быть практически любым. В данном случае мы используем свойство гомоморфизма, которое делает акцент на присутствие при управлении каких-то любых параметров в рамках заданной схемы управления, которые нужно соединить между собой так, чтобы получить системный эффект. Этот системный эффект в данной гомоморфной модели заключается в том, чтобы преодолеть дефолт фирмы. Факт преодоления дефолта заключается в том, что фирма может вернуть кредит вместе с процентами при заданных условиях возврата. Это еще одно гомоморфное условие, которое в каждой задаче может быть сформулировано по своему, как это и бывает на практике. Другими словами, мы имеем набор условий функционирования фирмы, которые содержат факты случайности (работают законы синергетики), факты изменения экономических показателей в определенных рамках (работают законы экономики), похожих на реальные ситуации управления, возможность в рамках определенных ограничений управлять этими процессами (работают законы кибернетики и менеджмента). На рис. 4 приведен информационное поле этой гомоморфной компьютерной модели.
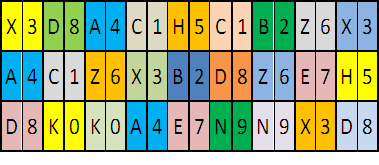
Рис. 4. Информационное поле гомоморфной компьютерной модели
На приведенной таблице цифры первого и второго слагаемого назначаются случайным образом, а сумма подсчитывается по правилам арифметики с одним условием слагаемые и сумма должны быть девятизначными. Это делается из условий простоты работы с моделью. Затем каждой цифре случайным образом ставится в соответствие случайная буква латинского алфавита. Затем цифры убираются и остаются только буквы (рис. 5).
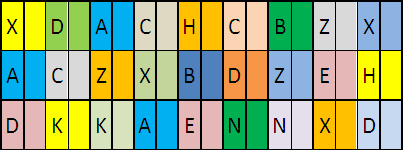
Рис. 5. Информационное поле готово к проведению эксперимента
Задача испытуемого заключается в том, чтобы назначить качественно оптимальную инвестицию и вставить качественно оптимальную цифру в выбранную клеточку, назначив, тем самым, числовое значение соответствующему параметру управления, который обозначен данной буквой. Если цифра назначена верно в рамках функционирования гомоморфной модели объекта управления, то инвестиция прибавляется к капиталу, если нет – то вычитается. После заполнения всех клеточек, это длится примерно 3 минуты, подводятся итоги. Если управление было максимально эффективным (качественно оптимальным), то дефолт будет преодолен, если нет, то дефолт будет иметь место и это будет зафиксировано в базе данных и сообщено посредством всплывающего информационного окна.
Построение качественно оптимальной стратегии управления объектом заключается в выявлении субстратных классов и соответствующих субстратов. В качестве субстратов выступаю самоорганизующиеся фракталы, которые обусловлены действующими в модели законами синергетики, заключающимися в том, что взаимодействие флуктуаций (случайных воздействий) и аттракторов (закономерностей) приводит в возникновению фракталов, от которых и зависит процесс оптимизации. Процесс моделирования сопровождается звуковыми эффектами и вызывает у студентов не только спортивный азарт, но и стремление освоить технологию качественной оптимизации стратегий управления.
На рис. 6 приведена база данных с результатами одного из тренингов.
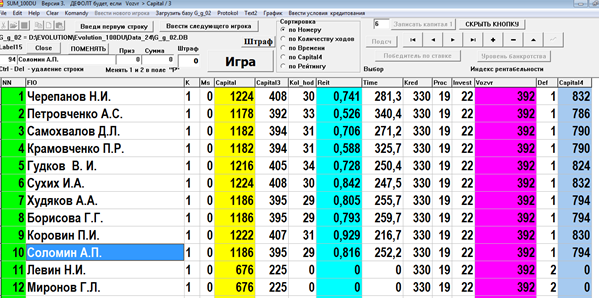
Рис. 6. База данных с результатами соревнования
Список литературы:
- Румянцев А.А. Метод и алгоритмы для решения прикладных контактных задач (системный подход). Отчет по НИР № 79077712. Кострома, 1979.
- Гагаев А.А. Теория и методология субстратного подхода в научном познании. Автореф. … дис. докт. филос. Наук.- М., 1994.
- Гагаев А.А. Теория и методология субстратного подхода в научном познании. — Саранск: Изд-во Мордов. Ун-та, 1994.-48с.
- Диалектико-формальный вариант общей теории систем: Отчет / Морд. Ун-т. Науч. рук. А.А. Румянцев, исп. А.А. Гагаев; № ГР 8108435; Инв. № Б 972365. Саранск, 1981. 58 с.
- Румянцев А.А., Гагаев А.А. Философско-методологические аспекты системного подхода в технике и социологии / Морд. Ун-т. Саранск, 1981. Деп. в ИНИОН АН СССР, 03.06.81. 1,5 п.л.
- Румянцев А.А. Эффективное управление: принятие обоснованных и оптимальных решений, интеллект и логика. Часть 1. Тесты – ООО «Контраст», Краматорск: 2003.-32 с.
- Философия управления обществом, провинцией, фирмой в этнокультурном и реформационном аспектах в теории и методологии субстратного подхода: Учеб. пособие/ ред.: А.А. Гагаев, А.А. Румянцев. — Саранск, 2009. — 696 с.
- Румянцев А.А. Оптимизирующий менеджмент: руководство по обучению и практическому применению.- Донецк.: Технопарк ДонНТУ УНИТЕХ, 2010, — 124 с.
- Румянцев А.А. Главная цель управления – структурно-субстратная оптимизация экономических показателей. Экономика современного предприятия, Октябрь, 2010. www.esp—izdat.ru
- Румянцев А.А. Субстратный подход – инструмент управления прогрессом в сфере философии, менеджмента, экономики, социологии, педагогики и психологии. Материалы электронной конференции по проблемам оптимизации управления. 2010 г.
- Румянцев А.А. Теоретические основы оптимального управления. Эл. Научный вестник КГТУ. 2010.- 11 с.
- Румянцев А.А. Субстратный подход к построению качественно оптимальных экономических доктрин. М., Научный эксперт. 3, 2011 г. Выпуск 3, стр. 16-31
- Румянцев А.А. Теория и практика субстратной оптимизации систем управления. Руководство по обучению и практическому применению. LAP LAMBERT Academic Publishing, 2013, 238 c.[schema type=»book» name=»СУБСТРАТНЫЙ ПОДХОД К ПОСТРОЕНИЮ КАЧЕСТВЕННО ОПТИМАЛЬНЫХ СИСТЕМ, ПРОЦЕССОВ И СТРАТЕГИЙ » description=»Разработано принципиально новое научное направление, которое называется субстратным подходом. Оно обладает предельной универсальностью своего практического применения, поскольку разработано на уровне философского знания. Целями субстратного подходя являются следующие: построение качественно оптимальных моделей, систем, процессов и стратегий в сфере управления, экономики, техники, математики, политики и в других областях деятельности. Методология и теория субстратного подхода включает в себя гносеологическую схему, всеобщий алгоритм движения по уровням абстрагирования и алгоритм достижения системного эффекта и качественной оптимизации целевой функции управления. Приведено дедуктивное обоснование субстратного подхода с помощью гносеологической схемы и индуктивное обоснование с помощью серии экспериментов на компьютерных и натурных моделях. Субстратный подход является революцией в науке, обладает мировым уровнем новизны и мировым уровнем значимости.» author=»Румянцев Анатолий Александрович » publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-01-08″ edition=»euroasia-science.ru_29-30.12.2015_12(21)» ebook=»yes» ]

