Процессы интеграции, происходящие во всех отраслях экономической деятельности, не обошли стороной и Россию, многие отечественные компании, как частные, так и государственные, активно перенимают зарубежные методы с целью повышения конкурентоспособности, роста рентабельности и стоимости предприятий.
В настоящее время одним из таких методов является стратегия слияния и поглощения предприятий.
В случае, если объединяемые компании-производители являются внутриотраслевыми конкурентами, становится важным, какой объем производства будет оптимален для каждого предприятия в условиях объединения.
То есть возникает вопрос: с какой мощностью должно работать предприятие, при условии, что с увеличением объема производства себестоимость единицы продукции уменьшается (за счет того, что постоянные затраты предприятия «разносятся» на большее количество произведенных единиц продукции).
График 1.
При этом также важно учитывать географию поставок (особенно в тех отраслях промышленности, где стоимость грузоперевозок имеет значительный вес).
Даннуюзадачу, учитывающую два этих фактора, можно решить с помощью нелинейной модели транспортной задачи.
Математическая модель задачи будет иметь следующую целевую функцию:


Таблица 1

Рассмотрим задачу на конкретном примере. При объединении двух конкурирующих предприятий необходимо оптимизировать производствограммонита.
Проведем анализ ретроспективных данных предприятий за 2005-2014 год в Excel. Данные были проранжированы по возрастанию количества тонн (Таблица 2). Далее строился график зависимости полной себестоимости продукции от объема производства. На графиках также отображены мнимые точки – симметричные реальным данным для получения точкиэкстремума.Затем была проведена аппроксимация полученных точек и получено уравнение(отражено в Таблице2, а также на Рис.1,2)
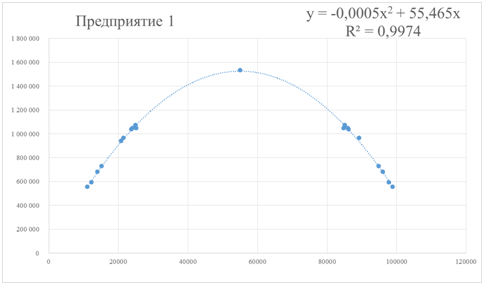
Рис.1
(для Предприятия 1)
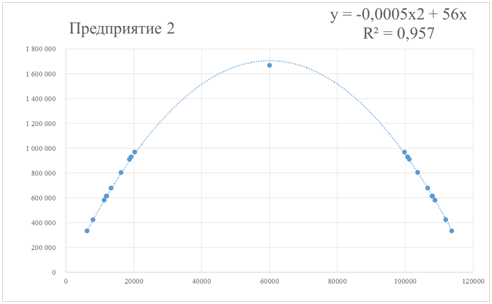
(для Предприятия 2)
Таблица 2
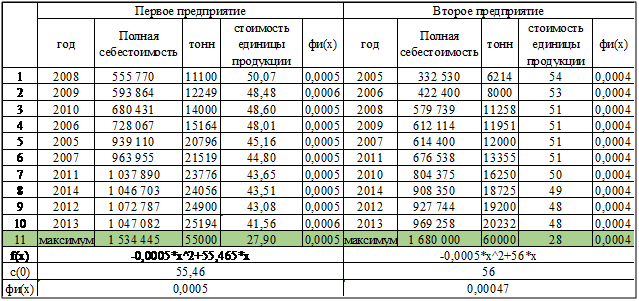
Далее, с(0) было рассчитано как производная функциив нулевой точке – в данном случае это значение55,46 и 56 соответственно для первого и второго предприятий.
Значениевычислялось из формулы (4). Функцияв данном случае принимает постоянное значение: для первого предприятия – это значение 0,0005,для второго – 0,00047.
После, была составлена Таблица 3 по аналогии с Таблицей 1 для решения транспортной задачи.
Задача решалась в программном обеспечении Rstudio симплекс-методом.
Алгоритм решения следующий: на первом этапе задача решалась только со значениями с(0), без учета. После полученного распределения объемов производства результаты использовались для расчета , и задача рассматривалась с новыми значениями, до тех пор, пока решения не совпадали.
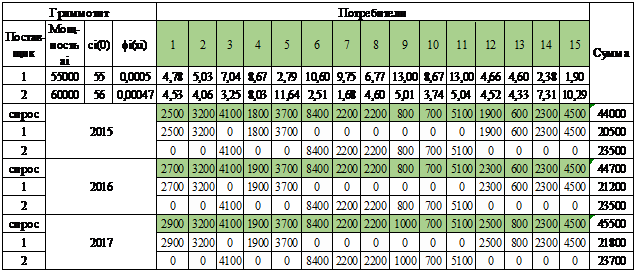
Таким образом, зная прогнозные значения спроса на граммонитпотребителейПредприятия 1 и Предприятия 2на 2015-2017 год, были получены оптимальные объемы производства в рамках объединения предприятий (результаты отражены в Таблице 3).
Таблица 3
Автор благодарит профессора Крянева А.В. за помощь при математической постановке рассмотренных в данной работе задач.
Список литературы:
- КоробовП.Н. «Математические методы и моделирование экономических процессов», Санкт-Петербург, 2002.-364с.
- «Справочник экономиста» №11, 2011.[schema type=»book» name=»ОЦЕНКА ЭКОНОМИЧЕСКОГО ЭФФЕКТА СЛИЯНИЯ ПРЕДПРИЯТИЙ» description=»В статье рассматривается расчет синергетического эффекта при объединениипредприятий одной отрасли путем оптимизации объемов производства. Для этого решалась транспортная задача при нелинейных затратах на производство, учитывающая снижение себестоимости единицы продукции при увеличении объемов производства.» author=»Карташева Мария Андреевна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-02-22″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_25.07.15_07(16)» ebook=»yes» ]

