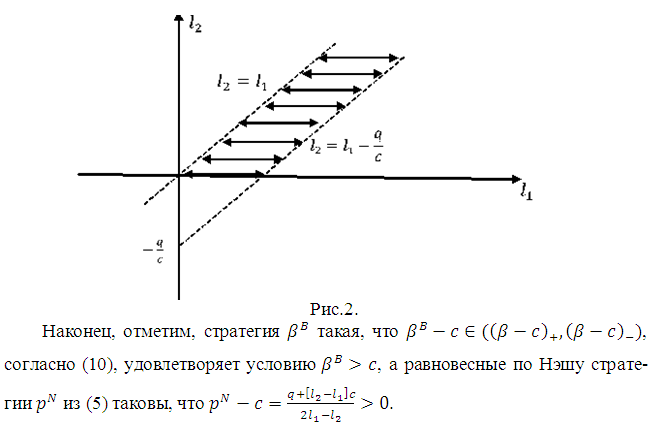
- Математическая модель
В 1883 г. французский математик Жозеф Луи Франсуа Бертран (1822-1900) построил модель [1] ценовой конкуренции на олигопольном рынке, на котором фирмы конкурируют между собой, меняя цену продукции. Заметим, что такая модель не «блистала новизной», ибо ровно на 45 лет раньше тоже французский экономист, философ и математик Антуан Огюст Курно (1801-1877) в «Исследовании математических принципов теории богатства» в разделе 7 «О конкуренции производителей» [2] рассмотрел частный случай олигополии – дуополию (участвуют только два производителя). В ней уже математическая модель основывалась на том, что оба производителя выбирают объем поставляемой продукции, цена же варьируется в результате равновесия между спросом и предложением. Рыночная цена устанавливается на том же уровне, на котором покупателями будет предъявлен спрос на весь «выкинутый на рынок» товар. Однако Бертран основывался на более естественном поведении продавца, именно, на выборе им цены, а не количества «выброшенного» товара, как у Курно. («Цена – стоимость плюс разумное вознаграждение за угрызение совести при назначении цены» – иронизирует американский писатель Амброз Бирс (1842-1914)). Заметим, что покупатели обычно рассматривают продукцию одинакового назначения разных фирм как разные товары. Поэтому будем считать, что на рынок каждая фирма выходит со своим товаром, причем все эти товары взаимозаменяемы.








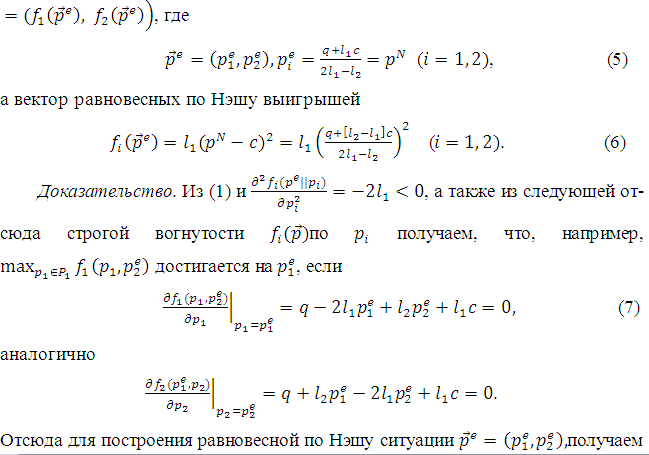






Список литературы.
- Bertrand J. Book review of theoriemathematique de la richessesociale and recherché sur les principles mathematiques de la theorie des richesses // Journal de Savants. – 1883. – V67. – P.499 – 508.
- Cournot A.A. Recherchersurles Principes Mathematiques de la Theorie des Rechesses. – Paris: L. Huchette, 1838.
- Nash J.F. Equilibrium point in N-person games // Proc. Nat. Academ. Sci. USA. – – 1950. – V.36. – P. 48-49.
- ВайсманК.С. Равновесие по Бержу: Автореф. дис. … канд. физ.-мат. наук. СПбГУ, 1995.
- Вайсман К.С. Равновесие по Бержу (раздел 3.2 из книги Жуковского В.И. и Чикрия А.А. «Линейно-квадратичные дифференциальные игры» Киев: Наукова Думка, 1994. – С. 119-142).
- I., SalukvadzeM.E. and VaismanK.S. The Berge Equilibrium: Preprint. Tbilisi: Institute of ControlSystem, 1994.
- Berge C. Theoriegenerale des jeuxa n personnes. Paris: Geurethier – Villars, 1957. (Русский перевод: Общая теория игр нескольких лиц. М.: Физматгиз, 1961).
- , Reviewof C. Berge “General theory of n-person games // Econometrica. – 1961. – 29. – P. 821.
- Жуковский В.И., Кудрявцев К.Н., Горбатов А.С. Равновесие по Бержу в модели олигополии Курно // Вестник Удмуртского университета. Серия Математика, Механика, Компьютерные науки. – – Т. 25. – №2. – С. 147-156.
- M., KörnerT.W., MusyO. And TazdaitT. Mutual supportin games: some propotues of Berge equilibria. // Journal of Mathematical Psychology, ArticleinPress. – 2011. – P. 1-10.
- Мащенко С.О. Концепция равновесия по Нэшу и ее развитие // Журнал обчисловальной та прикладноi математики. – 2012. – N – C. 40-61.
- Zhukovskiy Vladislav, Topchishvili Aleksander, Sachkov Sergey. Application of Probability of the Existence Problem of Berge-Vaisman Guarantied Equilibrium // Model Assisted Statistics and Applications. – 2014. – Vol. 9. – №3. – P. 223-239.
- Zhukovskiy V.I., Sachkov S.N. Bilanciamen to Conflitti Friendly // Italian Science Review. – 2014. – V. 18. – №9. – P. 169-179.
- Zhukovskiy V.I., Sachkov S.N., Gorbatov A.S. Mathemarical model of the “Golden rule” // Science, Technology and Life – 2014. Proc. Of the Internat. Scientific. Conf. CzechRepublic, KarlovyVary, 27-28 December 2014. –P. 16-23.
- Жуковский В.И., Чикрий А.А., Солдатова Н.Г. Равновесие по Бержу в конфликтах при неопределенности // В сб-ке 12 Всероссийского совещания по проблемам управления (электронный ресурс). – М.: 2014. Издательство: Институт проблем управления им. В.А.Трапезникова РАН. – С. 8290-8302.[schema type=»book» name=»АЛЬТРУИСТИЧЕСКОЕ РАВНОВЕСИЕ В КОНКУРЕНТНОЙ МОДЕЛИ ОЛИГОПОЛИИ БЕРТРАНА» description=»Найдены ограничения на параметры математической модели дуополии Бертрана, при которых участники конфликта получают большие выигрыши в ситуации равновесия по Бержу, чем в ситуации равновесия по Нэшу.» author=»Жуковский Владислав Иосифович, Макаркина Татьяна Владимировна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-02-08″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_29.08.15_08(17)» ebook=»yes» ]

