Ранее в своей статье автор показал, что для описания экономических процессов, происходящих в экономике страны можно применить теорию оболочек [2]. Кроме того в статьях автор также описал границы существования экономических оболочек малого, среднего и большого бизнеса, на которые могут воздействовать как внешние, так и внутренние силы [1, 3].
Валовой внутренний продукт ВВП (GDP) может быть исчислен следующими тремя методами:
- как сумма валовой добавленной стоимости (производственный метод);
- как сумма компонентов конечного использования (метод конечного использования);
- как сумма первичных доходов (распределительный метод).
При этом в расчетах могут быть использованы различные параметры такие как: потребление, инвестиции, правительственные расходы, экспорт, импорт и др. В представленном ниже материале при произведении вычислений была использована формула расчета объема экономической оболочки Veuc, которому соответствует ВВП страны т.е. Veuc (GDPc) = f(Х1, Х2, Х3, Х4). Здесь Х1, Х2, Х3 и Х4 параметры влияющие на ВВП страны.
Из анализа формулы можно определить характеристики параметров, влияющих на Veuc (GDPc), которые будут следующими:
- при увеличении параметра Х1 объем экономической оболочки Veuc увеличивается (GDPc);
- при увеличении параметра Х2 объем экономической оболочки Veuc (GDPc) увеличивается более интенсивно, чем от параметра Х1;
- при увеличении параметра Х3 объем экономической оболочки Veuc (GDPc) уменьшается;
- при увеличении параметра Х4 объем экономической оболочки Veuc (GDPc) увеличивается.
Следует сразу отметить, что при расчетах и построении рисунков параметры Х1, Х2, Х3 и Х4 могла бить величинами постоянными, уменьшаться или увеличиваться в 10 раз. На основе произведенных расчетов были построены графики, которые можно подразделить на следующие четыре группы:
- значения параметров Х1, Х2, Х3 и Х4 постоянные и увеличиваются;
- значения параметров Х1, Х2, Х3 и Х4 постоянные и уменьшаются;
- значения параметров Х1, Х2, Х3 и Х4 уменьшаются и увеличиваются;
- значения параметров Х1, Х2, Х3 и Х4 постоянные, уменьшающиеся и увеличивающиеся.
На рис. 1 представлен двухмерный график зависимости Veuc (GDPc) при Х1 = Х2 = 1, Х3 = 1…10. Х4 = 0,1…1, из которого видно, что значения Veuc вначале уменьшаются в 11,4 раза, а потом увеличиваются в 6,3 раза. На рис. 2 представлены два 3D-графика, которые дают более наглядно представить изменения Veuc. В этом случае нам целесообразно иметь значения крайних точек, т.к. при них величина Veuc т.е. ВВП будет максимальной.
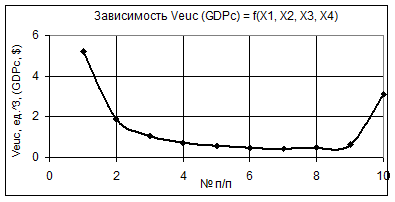
Рис. 1 Зависимость Veuc (GDPc) = f(Х1, Х2, Х3, Х4) при Х1 = Х2 = 1, Х3 = 1…10. Х4 = 0,1…1
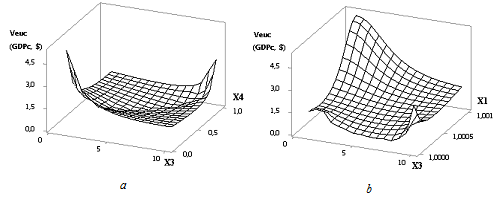
Рис. 2 3D-графики: a — Veuc (GDPc) = f(Х3, Х4); b — Veuc (GDPc) = f(Х3, Х1)
при Х1 = Х2 = 1, Х3 = 1…10, Х4 = 0,1…1
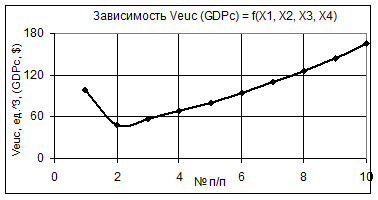
Рис. 3 Зависимость Veuc (GDPc) = f(Х1, Х2, Х3, Х4) при Х1 = 1, Х2 = Х3 = 1…10, Х4 = 1…0,1
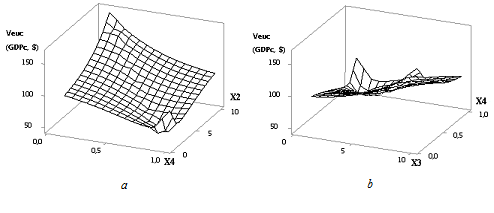
Рис. 4 3D-графики: a — Veuc (GDPc) = f(Х4, Х2); b — Veuc (GDPc) = f(Х3, Х4)
при Х1 = 1, Х2 = Х3 = 1…10, Х4 = 1…0,1
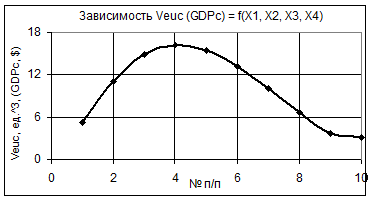
Рис. 5 Зависимость Veuc (GDPc) = f(Х1, Х2, Х3, Х4)
при Х1 = 1…10, Х2 = 1…0,1, Х3 = 1, Х4 = 0,1…1
Из следующего рис. 3 видно, что при Х1 = 1, Х2 = Х3 = 1…10, Х4 = 1…0,1 построенная кривая Veuc имеет спад в точке 2 после чего идет постепенный ее рост в 3,4 раза. На рис. 4 показаны два вида данной зависимости в виде трехмерных графиков. В данном примере нам надо брать значение параметров в точке 10, при которой будет максимальный объем экономической оболочки.
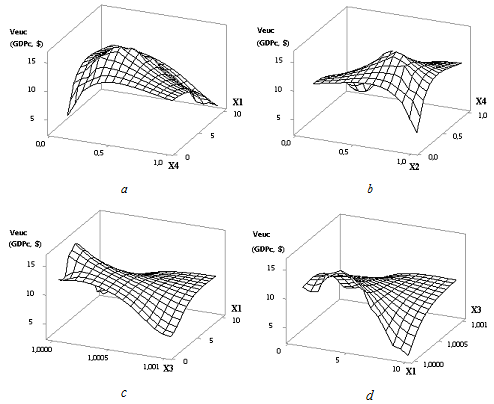
Рис. 6 3D-графики: a — Veuc (GDPc) = f(Х4, Х1); b — Veuc (GDPc) = f(Х2, Х4)
c — Veuc (GDPc) = f(Х3, Х1); d — Veuc (GDPc) = f(Х1, Х3)
при Х1 = 1…10, Х2 = 1…0,1, Х3 = 1, Х4 = 0,1…1
На рис. 5 мы можем видеть, что здесь построенная кривая Veuc имеет максимум в точке 4 после чего ее значения уменьшаются. Из чего можно сделать вывод, что нам выгодно иметь следующие значения параметров: Х1 = 4, Х2 = 0,7 и Х3 = 1, Х4 = 0,4, т.к. в этом случает экономика рассматриваемой страны будет иметь максимальное значение Veuc. Трехмерное изображение кривой Veuc, построенной на рис. 5, представлено в виде 4 поверхностей на рис. 6.
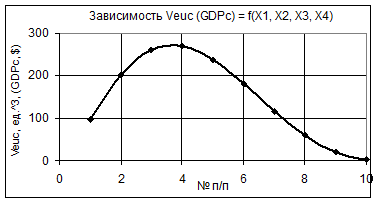
Рис. 7 Зависимость Veuc (GDPc) = f(Х1, Х2, Х3, Х4)
при Х1 = 1…10, Х2 = 1…0,1, Х3 = Х4 =1
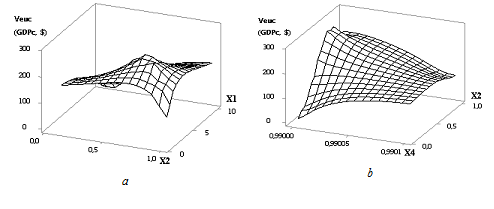
Рис. 8 3D-графики: a — Veuc (GDPc) = f(Х2, Х1); b — Veuc (GDPc) = f(Х4, Х2)
при Х1 = 1…10, Х2 = 1…0,1, Х3 = Х4 = 1
На рис. 7 построена практически аналогичная кривая Veuc как и на рис. 5, но в этом случае максимальное значение Veuc составляет уже 269, что в 16,6 раз больше. Следовательно, использовать следующие значения параметров Х1 = 4, Х2 = 0,7 и Х3 = 1 Х4 = 1 более выгодно. На рис. 8 показаны два примера 3D зависимости Veuc (GDPc) = f(Х1, Х2, Х3, Х4).
Как видно из рис. 9 здесь значение Veuc имеет самое большое из представленных выше примеров, т.е. Veuc = 8514,56 в точке 7 со значениями параметров: Х1 = 4, Х2 = 0,7 и Х3 = Х4 = 1. Здесь также представлен один 3D рисунок Veuc.
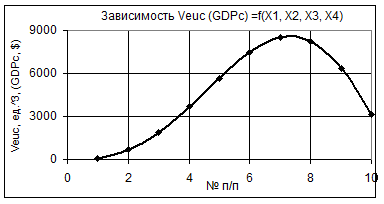
Рис. 9 Зависимость Veuc (GDPc) = f(Х1, Х2, Х3, Х4)
при Х1 = 1…0,1, Х2 = 1…10, Х3 = 1 Х4 = 1
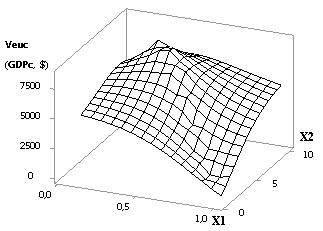
Рис. 10 3D-графики: a — Veuc (GDPc) = f(Х1, Х2) при Х1 = 1…0,1, Х2 = 1…10,
Х3 = Х4 =1
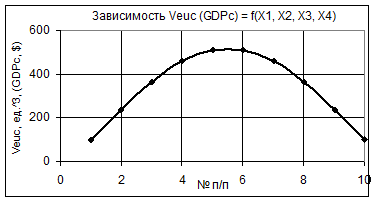
Рис. 11 Зависимость Veuc (GDPc) = f(Х1, Х2, Х3, Х4)
при Х1 = 1…0,1, Х2 = Х3 = 1…10, Х4 = 1
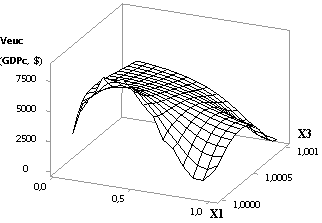
Рис. 12 3D-графики: a — Veuc (GDPc) = f(Х1, Х3) при Х1 = 1…0,1,
Х2 = Х3 = 1…10, Х4 = 1
Из следующего рис. 11 видно, что построенная кривая Veuc имеет максимальное значение Veuc = 509,87 и она симметрична относительно своего максимума. Рисунок 12 показывает, как изменяется построенная кривая Veuc в трехмерном пространстве.
После того как были произведены расчеты их результаты были сведены в общую таблицу, в которой были введены такие отношения как:
- Veucb…Veucf, где Veucb — начальное значение объема экономической оболочки, ед.3; Veucf — конечное значение объема экономической оболочки, ед.3;
- Veucf/Veucb — отношение конечного значения объема экономической оболочки к начальному.
Отношение конечного значения объема экономической оболочки Veucf к начальному Veucb показывает, во сколько раз увеличился (уменьшился) объем экономической оболочки, т.е. ВВП под воздействием на нее различных внешних сил. Следовательно, имея такие данные, мы можем выбрать такие параметры Х1, Х2, Х3 и Х4, при которых объем экономической оболочки останется неизменным или даже увеличится под воздействием внешних сил. То есть, тем самым при экономическом кризисе выбранные значения параметров позволят сохранить на прежнем уровне, или даже увеличить ВВП страны. После того, как была построена таблица ее преобразовали следующим образом — оставили только те значения, где Veucf /Veucb ≥ 1. На основе этого преобразования была получена окончательная таблица 1, часть которой представлена ниже. В таблицу 1 сведены только 17 вариантов, которые можно использовать при наступлении очередного экономического кризиса. Как видно из табл. 1 три варианта, при которых ВВП страны не изменится в период экономического кризиса, позволяют экономики страны остаться на докризисном уровне и дождаться окончания кризиса. Это варианты, где отношения Veucf /Veucb = 1.
Из всех остальных вариантов целесообразно применять те, где максимальное количество параметров Х1, Х2, Х3 и Х4 остаются неизменными, т.е. равны единицы. Например, вариант 4 имеет три параметра равные единице и позволяет увеличить ВВП в 18,73 раза при увеличении параметра Х4 в 10 раз.
Таблица 1
Статистика теоретических отношений Veucf /Veucb где Veucf /Veucb ≥ 1
| №
п/п |
Х1,
ед. |
Х2,
ед. |
Х3,
ед. |
Х4,
ед. |
Veucb… Veucf, ед.3
(GDРeucb…GDРeucf), $ |
Veucf /Veucb
GDРeucb / GDРeucf |
| 1. | 1 | 1 | 1…0,1 | 1 | 98,12…3102,97 | 31,62 |
| 2. | 1 | 1…10 | 1…10 | 1 | 98,12…3102,97 | 31,62 |
| 3. | 1…10 | 1 | 1 | 1 | 98,12…3102,97 | 31,62 |
| 4. | 1 | 1 | 1 | 0,1…1 | 5,24…98,12 | 18,73 |
| 5. | 1…0,1 | 1 | 1…0,1 | 0,1…1 | 5,24…98,12 | 18,73 |
| 6. | 1 | 1 | 1…0,1 | 1…0,1 | 14,5…165,63 | 11,42 |
| 7. | 1…0,1 | 1…10 | 1 | 1…0,1 | 98,12…512,7 | 5,22 |
| 8. | 1…0,1 | 1…10 | 1…10 | 1 | 98,12…509,87 | 5,20 |
| 9. | 1 | 1…10 | 1…10 | 1…0,1 | 53,61…165,63 | 3,45 |
| 10. | 1…10 | 1 | 1 | 1…0,1 | 48,07…165,63 | 3,45 |
| 11. | 1…10 | 1…0,1 | 1 | 0,1…1 | 5,24…16,21 | 3,10 |
| 12. | 1…10 | 1…0,1 | 1 | 1 | 98,12…269,25 | 2,74 |
| 13. | 1 | 1…0,1 | 1…0,1 | 0,1…1 | 1,52…3,1 | 2,04 |
| 14. | 1…0,1 | 1 | 1 | 0,1…1 | 1,52…3,1 | 2,04 |
| 15. | 1 | 1 | 1 | 1 | 98,12…98,12 | 1,0 |
| 16. | 1…10 | 1 | 1…10 | 1 | 98,12…98,12 | 1,0 |
| 17. | 1…0,1 | 1 | 1…0,1 | 1 | 98,12…98,12 | 1,0 |
Список литературы:
- Пиль Э.А. Границы существования экономических оболочек. Альманах современной науки и образования. 2008. №3. С.142-145
- Пиль Э.А. Применение теории и оболочек для описания процессов, происходящих в экономике. Альманах современной науки и образования. 2009. №3. С. 137-
- Пиль Э.А. Влияние различных переменных на экономическую оболочку страны. Альманах современной науки и образования. 2012. №12 (67). С. 123-126[schema type=»book» name=»ПУТИ ВЫХОДА ИЗ ФИНАНСОВОГО КРИЗИСА» description=»В статье предлагается теория финансовых кризисов, которые постоянно развиваются в современном обществе и охватывают в большей или меньшей степени практически все страны мира. На основе расчетов автор построил двух и трехмерные графики, которые более точно показывают влияние различных параметров на ВВП страны. Произведенные расчеты позволили построить таблицу и выявить варианты выхода из экономического кризиса.» author=»Пиль Эдуард Анатольевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-03-08″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_27.06.2015_06(15)» ebook=»yes» ]

