Существует два типа вооруженного противоборства [6]:
- Вооруженное противоборство первого типа, включающее:
− нанесение ударов по обороняемому объекту противника, который является относительно самостоятельным, физически изолированным от боевой системы противника;
− отражение ударов противника по своему обороняемому объекту, который также является относительно самостоятельным, физически изолированным от своей боевой системы.
Этот тип противоборства характерен для систем оперативного и стратегического уровней, когда каждая из противоборствующих группировок сил, боевых систем, выполняет задачи нанесения поражения критически важным объектам противника, защищаемых его боевой системой.
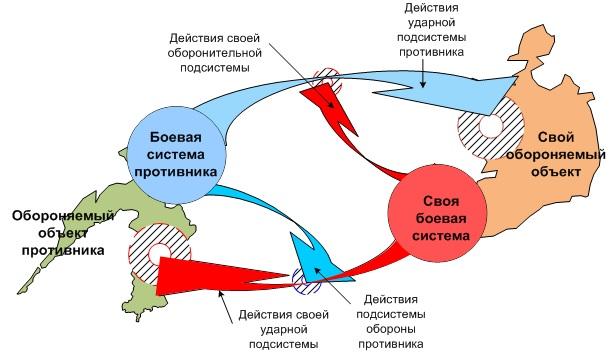
Рисунок 1. Вооруженное противоборство боевых систем с нанесением ударов по обороняемым объектам, которые являются относительно самостоятельными, физически изолированными от боевых систем
ОЛВМ вооруженное противоборство такого типа описывает и оценивает с помощью СФЦ корректно [6].
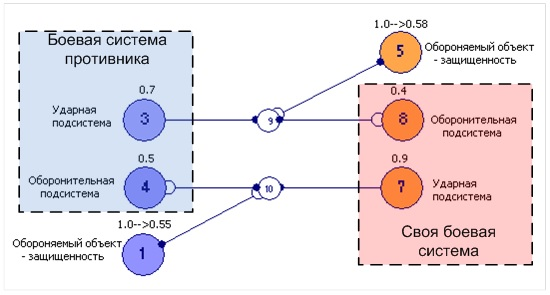
Рисунок 2. Корректное представление вооруженного противоборства с помощью СФЦ ОЛВМ
- Вооруженное противоборство второго типа, типа дуэли, включающее:
− нанесение ударов непосредственно по боевой системе противника;
− отражение ударов противника по своей боевой системе.
Этот тип противоборства характерен для боя кораблей, истребителей, танков, дуэли стрелков, т.е. для тактических форм применения сил.
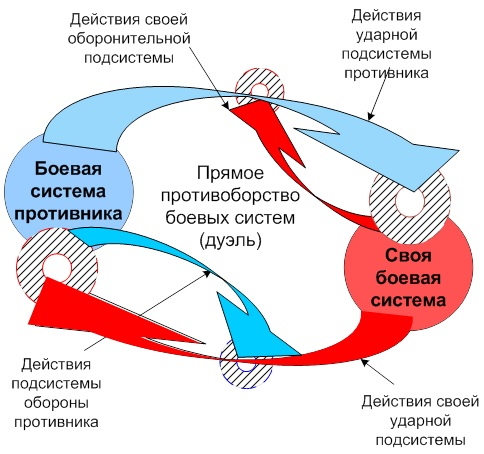
Рисунок 3. Вооруженное противоборство боевых систем типа дуэли с нанесением ударов непосредственно по боевой системе противника и отражением ударов противника по своей боевой системе
ОЛВМ вооруженное противоборство такого типа в комбинаторном представлении, как показано на СФЦ, описывает и оценивает некорректно.
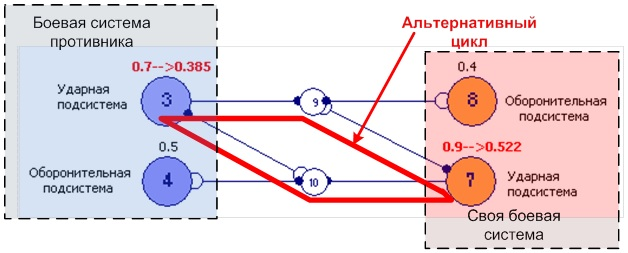
Рисунок 4. Некорректное представление вооруженного противоборства типа дуэли с помощью СФЦ ОЛВМ
И дело здесь не в самой информационной технологии, а в том, что имеет место итеративная схема расчета конечных состояний сторон, определяемая уравнениями Ланчестера для простейшей схемы вооруженного противоборства [1].
Уравнения динамики боя Ланчестера описываются поведением точки положительного квадранта плоскости. В данном случае используется упрощенная модель. Переменные х и у отражают численности борющихся сторон. Модель имеет вид:
 |
(1) |
За единицу времени dt каждая тактическая единица стороны х уничтожает а тактических единиц стороны y, и обратно, каждая тактическая единица стороны y уничтожает в тактических единиц стороны х.
Решение уравнений динамики боя осуществляется посредством их интегрирования:
 |
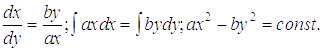(2) |
Изменение численностей сил (войск) сторон происходит вдоль гиперболы, определенной этим уравнением (рис. 5).
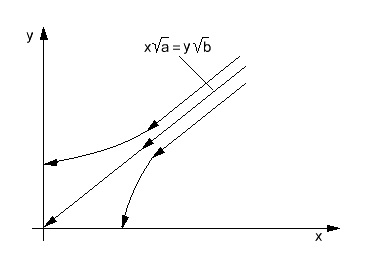
Рисунок 5. Графическая интерпретация решения уравнений Ланчестера
Если исходная точка находится ниже диагональной траектории, то победу одерживает сторона х, а если выше, то сторона у. Таким образом, такого рода модель приводит к исходу, характеризующемуся полным истреблением сил (войск) одной из сторон в результате тотальной войны на уничтожение.
Однако реальная постановка задачи на практике связана, во-первых, с дополнительным учетом противодействия ударам сторон, что приводит к снижению их ударного потенциала, во-вторых, с кратковременным, а не беспредельным, обменом ударами, что приводит к претерпеванию сторонами лишь частичного ущерба.
Рассматривая в исходной постановке одностороннее нанесение сторонами ударов с учетом противодействия, получим следующие оценки математических ожиданий доли пораженных сил (войск) сторон
 |
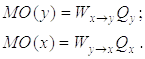(3) |
Здесь 
– вероятности поражения сторон взаимными ударами; 
– вероятности преодоления противодействия оборонительных подсистем сторон.
Приближенность такого расчета показателей исхода боевого столкновения состоит в том, что они учитывают лишь часть противодействия, состоящего в реализации показателей стойкости ударных подсистем к воздействию поражающих факторов [8]. Но боевые системы состоят из совокупностей ударных и оборонительных подсистем. Поэтому имеет место и ущерб, претерпеваемый оборонительными подсистемами от огневого поражения ударных подсистем противника, который в формулах (3) не учитывается. Как результат, они приводят к завышению расчетных показателей.
Для устранения этой методической погрешности необходимо перейти к итеративному расчету:
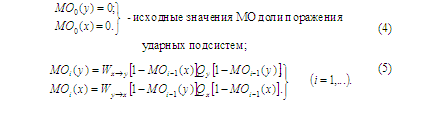
Произведения 
и характеризуют ударный потенциал стороны х и оборонительный потенциал стороны у с учетом потерь сил (войск) ударной подсистемы стороны х и оборонительной подсистемы стороны у.
В итерациях вычисляются показатели МО доли пораженного потенциала, т.е. численности сил (войск) сторон, при условии, что ударную задачу выполняют и противодействие оказывают боевые системы с оценками ущерба, рассчитанными в предыдущих итерациях. Соответственно, в итерациях потенциалы поражения и противодействия уменьшаются пропорционально снижению боеспособности боевых систем, т.е. уменьшению численности сил (войск) сторон в целом.Произведения и характеризуют ударный потенциал стороны х и оборонительный потенциал стороны у с учетом потерь сил (войск) ударной подсистемы стороны х и оборонительной подсистемы стороны у.
Итерационный процесс является сходящимся. С помощью математической модели (5), реализованной в среде программного комплекса Mathcad, получены следующие графики расчетных показателей (рис. 6).
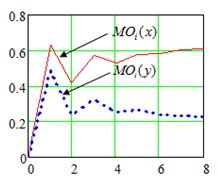
Рисунок 6. Сходимость итерационного процесса уточнения значений оценок показателей исхода боевого столкновения
Как следует из графиков, итерационный процесс быстро затухает, так что с приемлемой погрешностью (в данном случае 7…9%) достаточно ограничиться двумя итерациями.
Задача состоит в том, чтобы эти результаты получить с примененем средств моделирования ОЛВМ, отражая взаимозависимость исходов ударов и противодействия и избегая при этом альтернативного цикла. Монография [6] ответа на этот вопрос не дает, рекомендуя лишь отказываться от ОЛВМ-моделирования данного варианта боевого столкновения. Высокий научный уровень монографии, в которой не дан ответ на вопрос о способе ОЛВМ-моделирования альтернативного цикла, ставит этот вопрос в разряд проблемных.
Вместе с тем, данная постановка задачи является практической, например, при оценке соотношения сил сторон и возможных последствий боевого столкновения своих сил (войск) с противником [7].
Для разрешения проблемы альтернативного цикла с применением ОЛВМ можно использовать прием, рассмотренный выше, а именно путем итерационного расчета показателей.
Вариант схемы функциональной целостности (СФЦ) модели боевого столкновения типа дуэли с разделением альтернативного цикла по итерационным ветвям, с отражением только первой и второй итераций, представлен на рис. 7.
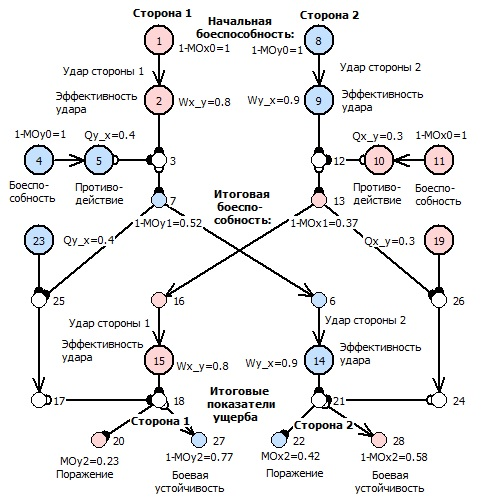
Рисунок 6. Схема функциональной целостности с разделением ветвей альтернативного цикла
Как видно, по показателям математического ожидания доли наносимого ущерба 
ОЛВМ-модель развязки альтернативного цикла точно повторяет результаты расчета по итогам двух циклов в математической модели, реализованной в среде программного комплекса Mathcad.
Дальнейшее итерационное уточнение значений вычисляемых показателей может быть достигнуто путем дополнения СФЦ на рис. 6 еще одним итерационным циклом. Порядок решения этой задачи показан выше, поэтому решение вопроса о необходимости усложнения СФЦ для повышения точности оценок остается за пользователем
Таким образом, решена проблемная задача разработки ОЛВМ-модели вооруженного противоборства боевых систем тактического уровня с нанесением ударов непосредственно по боевой системе противника и отражением ударов противника по своей боевой системе. Постановки задач моделирования и расчетов боевых столкновений дуэльного типа встречаются в теории [3, 4, 5] и на практике, так что полученное решение проблемы альтернативного цикла для ОЛВМ является актуальным.
Литература:
- Аналитическое моделирование в прогнозировании и планировании. – Интернет-ресурс .
- АРБИТР, Программный комплекс автоматизированного структурно-логического моделирования и расчета надежности и безопасности систем (ПК АСМ СЗМА), базовая версия 1.0; ПК АСМ 2001 / А.С. Можаев / ОАО «СПИК СЗМА». − М.: РОСПАТЕНТ РФ, 2003.
- Вентцель Е.С. Исследование операций: задачи, принципы, методология. – М.: Наука, 1980. – 208 с.
- Волгин Н.С., Махров Н.В., Юровский В.А. Исследование операций. В трех частях. – Л.: ВМА, 1978 – 1982.
- Динер И.Я. Методы исследования операций. Выпуск 2. Основы теории эффективности. − Л.: ВМОЛА, 1965. −232 с.
- Применение общего логико-вероятностного метода для анализа технических, военных организационно-функциональных систем и вооруженного противоборства // Монография, научное издание / В.И. Поленин, И.А. Рябинин, С.К. Свирин, И.А. Гладкова. Под ред. А.С. Можаева. – СПб: СПб-региональное отделение РАЕН, 2011. − 416 с.
- Пучнин В.В. Словарь терминов оперативного искусства. – СПб: Военно-морская академия им. Н.Г. Кузнецова, 2003.
- Унифицированные структурные схемы функционирования элементов структурно-сложных объектов с отражением влияния неблагоприятных и поражающих факторов В.И. Поленин, Н.А. Махутов, А.А. Потехин – СПб: Морская радиоэлектроника, №1 (51), 2015. – С. 50-53.[schema type=»book» name=»РАЗРАБОТКА МОДЕЛИ ВООРУЖЕННОГО ПРОТИВОБОРСТВА БОЕВЫХ СИСТЕМ ТАКТИЧЕСКОГО УРОВНЯ С НАНЕСЕНИЕМ УДАРОВ НЕПОСРЕДСТВЕННО ПО БОЕВОЙ СИСТЕМЕ ПРОТИВНИКА И ОТРАЖЕНИЕМ УДАРОВ ПРОТИВНИКА ПО СВОЕЙ БОЕВОЙ СИСТЕМЕ» description=»В статье рассмотрены постановка и решение проблемной задачи разработки методических основ формирования модели вооруженного противоборства боевых систем тактического уровня. Для этого уровня характерны нанесение ударов непосредственно по боевой системе противника и отражение ударов противника по своей боевой системе. Проблематичность решения задачи объясняется методическим препятствием в форме альтернативного цикла, не позволяющего получить значения показателей прямым расчетом. Предложена процедура расчета на сходящемся итеративном процессе. Приводится решение задачи создания ОЛВМ-модели с реализацией двух итераций.» author=»Поленин Владимир Иванович, Сущенков Дмитрий Андреевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-02-08″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_29.08.15_08(17)» ebook=»yes» ]