Опытно-экспериментальная работа по реализации методического обеспечения математической подготовки проводилась на базе Шуйского филиала ОГБОУ СПО «Ивановский промышленно-экономический колледж» в период с 2012 по 2014 год. В работе были задействованы студенты 2 курса специальности 220703 Автоматизация технологических процессов и производств (по отраслям). Назовем группу студентов, обучавшуюся в 2012-2013 учебном году контрольной (КГ, количество студентов – 22), а в 2013-2014 – экспериментальной (ЭГ – количество студентов 24). Опытно-экспериментальная работа проводилась в три этапа: констатирующий, формирующий, контрольный.
Целью проведения первого этапа опытно-экспериментальной работы было выявление начального уровня математической подготовки обеих групп – контрольной и экспериментальной. Студентам был предложен тест по математике, содержащий задания, которые оценивались баллами от 0,3 до 0,5, а итоговая оценка за работу суммировалась.
Средний балл по КГ и ЭГ составляет соответственно 3,3 и 3,4 балла. Анализ полученных данных с использованием статистического критерия Вилкоксона-Манна-Уитни дает эмпирическое значение критерия 0,3185 (критическое 1,96), что позволяет сделать вывод: характеристики сравниваемых выборок совпадают на уровне значимости 0,05. Сводные данные с учетом перевода полученных баллов в оценки («2» – 0-2,4; «3» – 2,5-3,6; «4» – 3,7-4,4; «5» – 4,5-5,0) приведены на диаграмме (рис. 1).
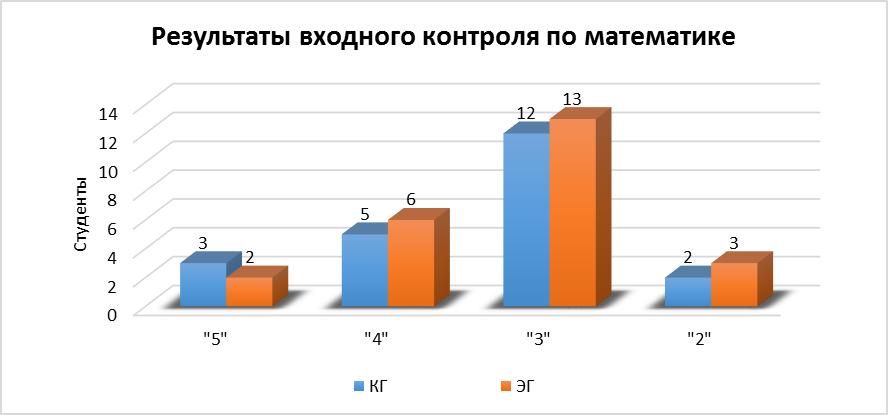
Рисунок 1. Входной контроль по математике в КГ и ЭГ
Качественная успеваемость в КГ и ЭГ составляет 36% и 33% соответственно, неуспевающие составляют 9% и 13% соответственно. Анализ начального уровня математических знаний в данных группах позволяет использовать данные выборки для последующей экспериментальной работы.
Также в исследуемых группах было проведено анкетирование студентов, целью которого было диагностика мотивационного компонента в процессе математической подготовки и изучения направленности студентов на дополнительную внеаудиторную работу по математике. Студентам было предложено выбрать 4 варианта ответа (a. Да, конечно; b. Скорее да, чем нет; c. Скорее нет, чем да; d. Нет) на следующие вопросы: 1) является ли математика одним из самых любимых предметов? 2) Важно ли хорошо знать математику для Вашей будущей профессии? 3) Хотите ли Вы работать над дополнительными проектами по математике?
На рисунке 2 представлены результаты анкетирования по контрольной группе до начала экспериментальной работы.
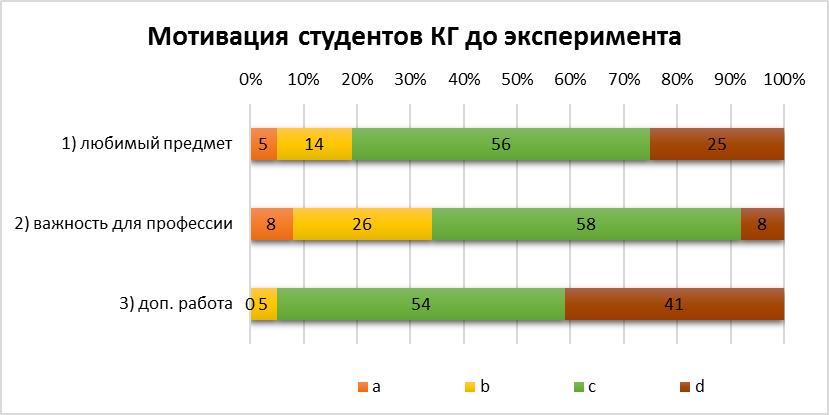
Рисунок 2. Структура мотивации студентов КГ до эксперимента
Ответы a и b являются наиболее предпочтительными с точки зрения мотивации обучения математике. Из диаграммы видно, что по каждому из трех вопросов такие ответы составляют соответственно 19%, 34%, 5%. Характерно, что важность для профессии не осознают 64% опрошенных. Рассмотрим аналогичные данные по экспериментальной группе (см. рис. 3).
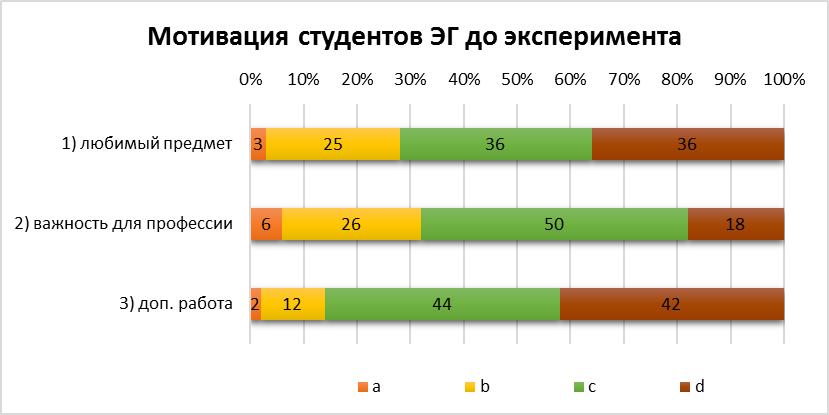
Рисунок 3. Структура мотивации студентов ЭГ до эксперимента
В целом структура мотивации по данной группе студентов совпадает с контрольной. Хорошо выраженная направленность на изучение математики есть не более чем у 32% студентов. Важность изучения математики для будущей профессии не понимают 68% опрошенных.
Целью проведения второго этапа (формирующего) опытно-экспериментальной работы было внедрение в учебный процесс разработанного нами методического обеспечения, организация математической подготовки студентов в соответствии с теоретически обоснованной моделью математической подготовки студентов промышленно-экономического колледжа. В рамках данного этапа опытно-экспериментальной работы были проведены лекции и практические занятия со студентами экспериментальной группы в объеме, предусмотренном рабочей программой по математике.
Рассмотрим методику организации работы со студентами ЭГ в соответствии с поставленными задачами. Электронный учебно-методические комплекс был предоставлен для использования студентами как во время аудиторных занятий, так и для самостоятельной работы. При изучении теоретического материала во время проведения аудиторных занятий ЭУМК использовался для организации фронтальной работы со студентами при объяснении, а также для организации индивидуальной работы с учебным материалом, самостоятельной работы по составлению конспектов [3, с.23].
При организации практических занятий по математике применялись разработанные нами дидактические материалы, имеющие 4 уровня освоения практического занятия. Оценка выполнения каждого уровня также нашла отражение в рейтинговой системе [1, с. 22].
Использование автоматизированной системы обработки данных успеваемости студентов и выделение отдельных компонентов формируемой математической компетентности позволяет оперативно и наглядно прослеживать индивидуальный образовательный маршрут студентов ЭГ. Нами были составлены диаграммы, отражающие уровень сформированности отдельных компонентов математической компетентности на момент завершения 1 модуля и 2 модуля соответственно (рис. 4 и 5 соответственно).
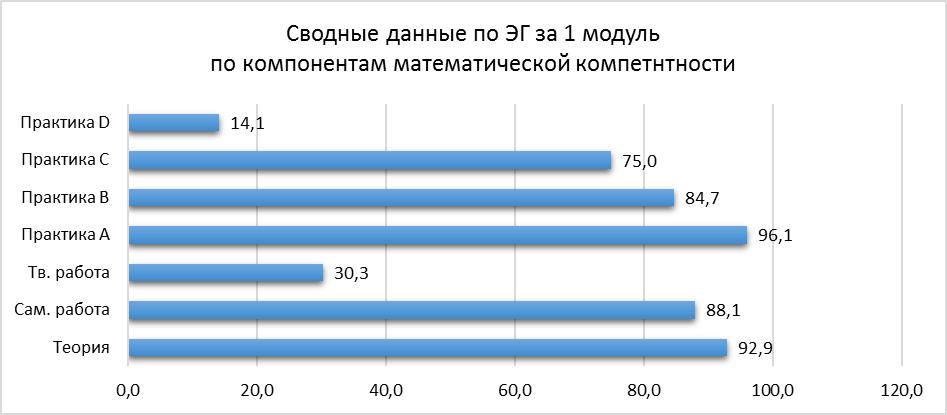
Рисунок 4. Успеваемость студентов ЭГ по окончании 1 модуля
Своевременный анализ этих данных в ходе экспериментальной работы позволил увидеть следующие тенденции в процессе математической подготовки. Менее активны студенты при выполнении практических заданий повышенного уровня и не стремятся использовать возможность для повышения рейтинга через выполнение дополнительных заданий, творческих работ, проектной деятельности. Также видно, что более успешны студенты ЭГ при выполнении практических заданий базового уровня. Неплохие показатели по теоретическому компоненту и самостоятельной работе. На рис. 5. показаны аналогичные данные по результатам 2 модуля.
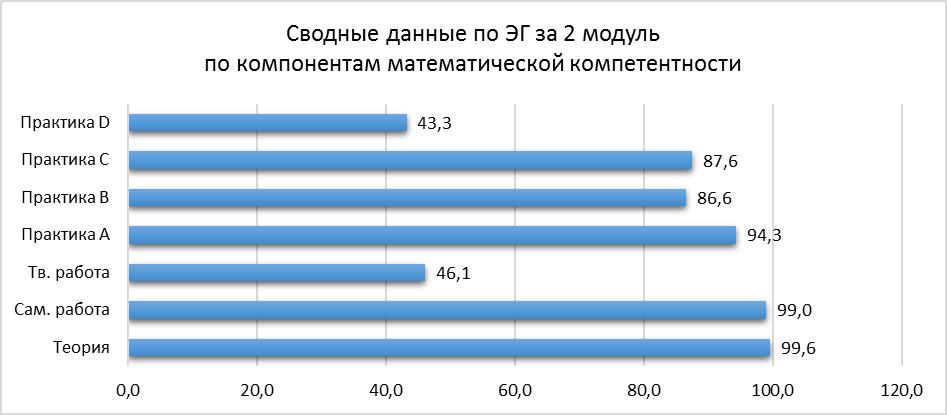
Рисунок 5. Успеваемость студентов ЭГ по окончании 2 модуля
На диаграмме видно, что сводные данные по менее выраженным по уровню сформированности компонентам выросли, но все же остаются не так высоки. Итоги 2 модуля показали, что успешность выполнения заданий профессионального уровня выросла с 75,0 до 87,6 баллов и немного превысила показатель «Практика В» (86,6 балла).
В ходе экспериментальной педагогической работы отслеживалась динамика формирования уровней отдельных компонентов математической компетентности каждого студента. На рисунке 6 хорошо видны сдвиги в уровнях сформированности этих компонентов результатам двух модулей изучаемого курса математики.
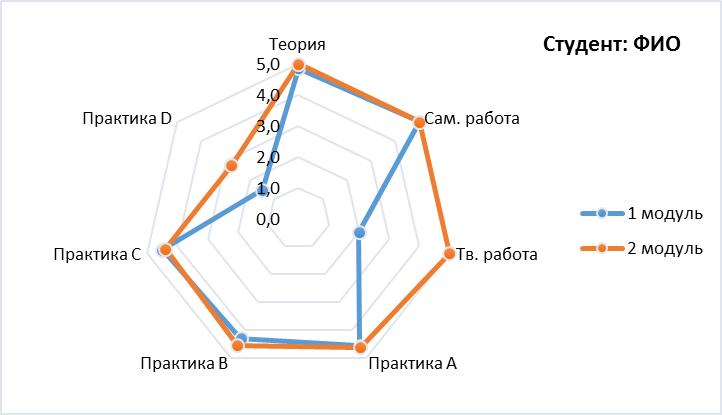
Рисунок 6. Динамика формирования компонентов
математической компетентности студента
Одна из важных задач, стоящих перед формирующим этапом экспериментальной работы – организация проектной и научно-исследовательской деятельности. Для организации проектной деятельности мы выбрали такое направление как создание электронных образовательных ресурсов (ЭОР) по математике в среде программирования Visual Basic. Такой проект носит комплексный междисциплинарный характер. Конечным результатом, продуктом деятельности студента становится исполняемая программа по выбранной теме, которая работает в операционной системе Windows независимо от установленного программного обеспечения [2, с. 26].
Третий этап опытно-экспериментальной работы – анализ полученных образовательных результатов, оформление выводов. По окончании изучения курса математики мы вновь предложили испытуемым ответить на вопросы анкеты. Вот какие результаты можно видеть у контрольной группы (см. рис. 7).
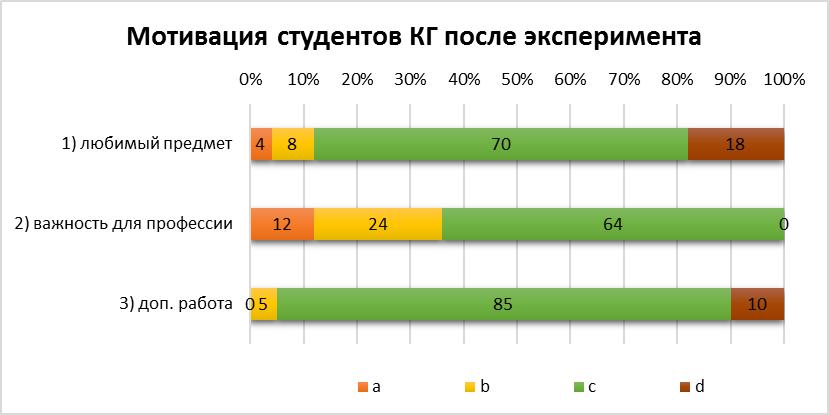
Рисунок 7. Структура мотивации студентов КГ после эксперимента
Из диаграммы видно, что изменилось понимание важности математики в профессиональной деятельности. Не осталось студентов, которые сказали бы категорическое «нет» (ответ d). Но процент хорошо осознающих необходимость математических знаний составляет 36%. Существенно уменьшилась направленность на дополнительную творческую работу по дисциплине: 95% студентов ответили «скорее нет, чем да». Рассмотрим результаты анкетирования экспериментальной группы (см. рис. 8).
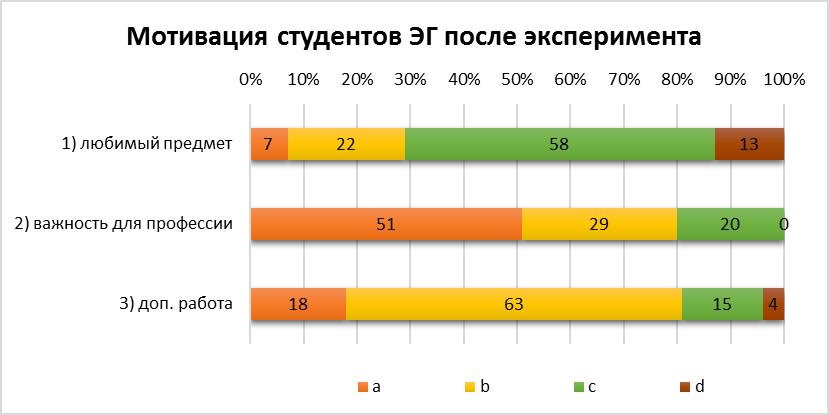
Рисунок 8. Структура мотивации студентов ЭГ после эксперимента
Анализ ответов на вопрос 2 и 3 показывает, что существенно изменилась структура мотивации студентов в изучении математики. Важность данной дисциплины признают все студенты, а более безоговорочно – 80% (рост на 48%). Дополнительную активность в процессе математической подготовки желает проявлять 81% опрошенных (рост 67%). Таким образом, можно сделать вывод, что внедрение разработанной модели математической подготовки, включающей в себя мотивационный компонент как составляющую математической компетентности, имеет положительный результат.
Сопоставим данные, полученные в результате автоматизированной обработки первичных рейтинговых оценок студентов ЭГ за 4 среза: входной контроль, 1 модуль, 2 модуль и итог. На основании этих данных составим следующую таблицу отображающую динамику результатов студентов ЭГ (см. таблица 1) и представим в виде диаграммы (см. рис. 9).
Таблица 1
Динамика успеваемости студентов ЭГ
| Уровень сформированности математической компетентности | Оценка |
Количество студентов, % |
|||
| входной контроль | 1 модуль | 2 модуль | итоговый контроль | ||
| Высокий | «5» | 8 | 4 | 25 | 25 |
| Выше допустимого | «4» | 25 | 33 | 21 | 21 |
| Допустимый | «3» | 54 | 46 | 50 | 50 |
| Низкий | «2» | 13 | 17 | 4 | 4 |
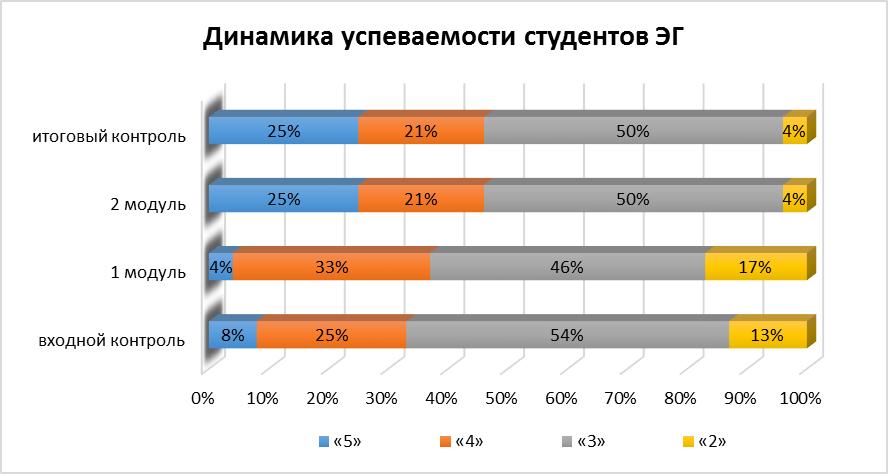
Рисунок 9. Динамика успеваемости студентов ЭГ
Из графика видно, что качественная успеваемость студентов, у которых математическая компетентность достигла высокого и выше допустимого уровня, выросла с 33% до 46%, а студентов с низким уровнем математической компетентности стало меньше с начала экспериментальной работы на 9%. Больший процент студентов ЭГ имеют допустимый уровень математической компетентности и это соотношение изменилось в ходе математической подготовки несущественно – с 54% до 50%. Небольшое увеличение неуспевающих студентов наблюдается по окончании 1 модуля.
Сравним результаты входного и итогового контроля знаний по математике в контрольной и экспериментальной группах (см. таблицу 2).
Таблица 2
Результаты входного и итогового контроля знаний по математике
| Оценки | До эксперимента | После эксперимента | ||
| КГ, % | ЭГ, % | КГ, % | ЭГ, % | |
| «5» | 13 | 8 | 14 | 25 |
| «4» | 23 | 25 | 23 | 21 |
| «3» | 55 | 54 | 58 | 50 |
| «2» | 9 | 13 | 5 | 4 |
Отразим данные, полученные на контрольном этапе экспериментальной работы в виде диаграммы. (см. рис. 10).
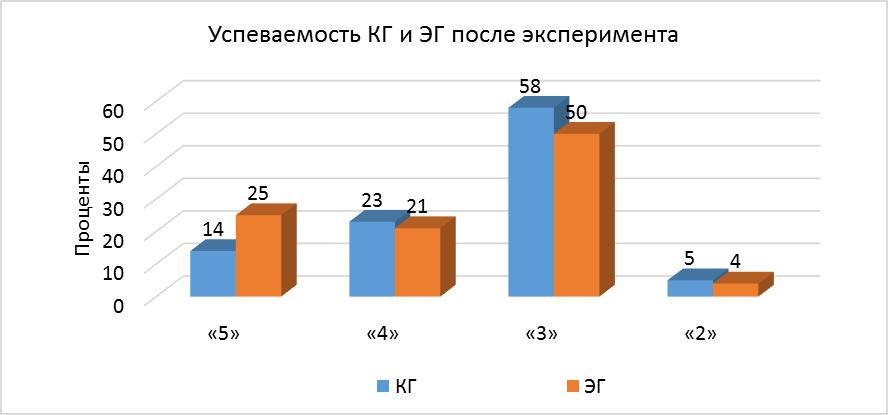Рисунок 10. Успеваемость студентов КГ и ЭГ после эксперимента
Данные диаграммы показывают, что качественная успеваемость студентов ЭГ чуть выше, чем в КГ – 46% и 37% соответственно. Большую долю в обеих группах составляют студенты, имеющие оценку «3». Применение статистического критерия Вилкоксона-Манна-Уитни (эмпирическое значение – 1,7592, критическое – 1,96) показывает, что характеристики сравниваемых выборок совпадают на уровне значимости 0,05, т.е. рассматриваемые нами группы статистически не различаются.
Таким образом, мы можем делать вывод, что методика реализации модели математической подготовки имеет положительную динамику образовательных результатов студентов, а значит может быть использована в учебном процессе, ее жизнеспособность, доказывается результатами опытно-экспериментальной работы.
Список литературы:
- Кашинцева, Л.Н. Математическая подготовка студентов колледжа в условиях внедрения новых образовательных стандартов [Текст] / Л.Н. Кашинцева //Научный поиск. – 2012. – №4.4. – С. 21-23.
- Кашинцева, Л.Н. Проектная деятельность по математике как средство формирования общих и профессиональных компетенций студентов колледжа [Текст] /Л.Н. Кашинцева //Научный поиск. – 2013. – №2.4 – С. 26-28.
- Кашинцева, Л.Н. Создание и использование электронных образовательных ресурсов в процессе математической подготовки студентов колледжа [Текст] / Л.Н. Кашинцева //Научный поиск. – 2014. — № 2.2. – С. 22-25[schema type=»book» name=»МАТЕМАТИЧЕСКАЯ ПОДГОТОВКА БУДУЩИХ ТЕХНИКОВ: РЕЗУЛЬТАТЫ ОПЫТНО-ЭКСПЕРИМЕНТАЛЬНОЙ РАБОТЫ» description=»В статье описаны основные этапы и результаты опытно-экспериментальной работы по реализации методического обеспечения математической подготовки студентов технического колледжа. » author=»Кашинцева Любовь Николаевна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-02-27″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_25.07.15_07(16)» ebook=»yes» ]