Example 1

2.We find asymptotes of the function: as function is continuous on an interval , then vertical asymptotes are absent.
Let us now find the slant asymptotes:
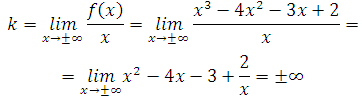
The slant asymptotes are absent.
Thus, function isn’t limited from above and not limited from below.
- Zeroes of function and intervals of constancy of signs.
- a) At first we will find a point where function crosses ordinate axis:

We will substitute number in the equation, such as
To be clear, we put all of these numbers, and then we will do a conclusion
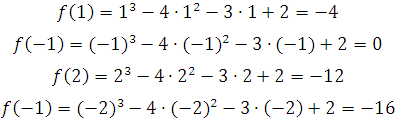
As we see from our answers, we are satisfied by number , at which function will be equals to zero.

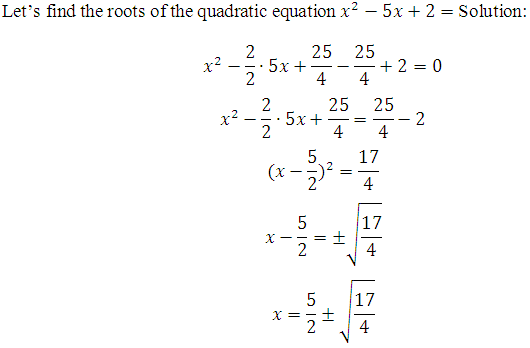

We will postpone them on a number line and we will define derivative signs:
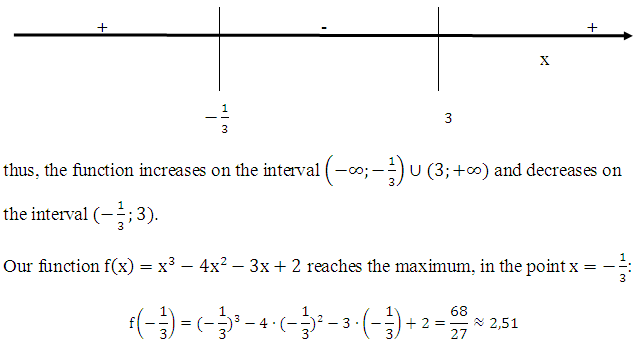


The curve has point of inflection.
- Construct the graph of the function
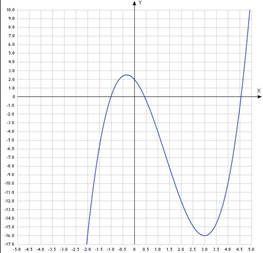
Figure 1
Example 2

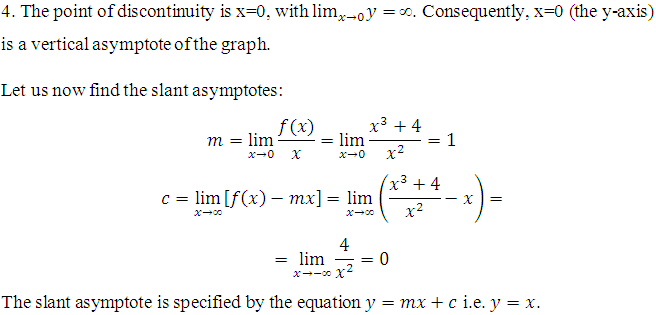
- Let us find the extremum of the function and the intervals of monotonicity.

6) Now we find the intervals of concavity of the curve and its points of inflection. Since, , the graph of the function is concave up everywhere. The curve has no point of inflection.
Using the above analysis, we construct the graph of the function.
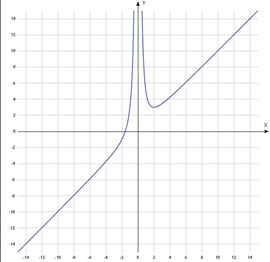
Figure 2
List of References
- Vinay Kumar. Function and Graphs for IIT JEE., New Delli 2013
- A.N. Kolmogorov. Algebra and beginning mathematical analysis. 10-11. Moscow 2008
- V.V. Konev. The elements of mathematics., Tomsk 2009
- Mathematics, Basic math and Algebra, Navedtra 1985[schema type=»book» name=»TO INVESTIGATE OF ALGEBRAIC FUNCTIONS» description=»In this article is considered scheme of investigate of algebraic functions. Proposed elementary (with the use of derivative) way to study the function. This method makes it possible to obtain an auxiliary function, which is the derivative. As a result, the most difficult stage of finding gaps increase (decrease) and the extreme points is avoidable to explore the elements of mathematical analysis. This opens up many other methodological features that are implemented in this article. This article will be useful to students and teachers of mathematical disciplines of pedagogical universities.» author=»Баетов Каирден Хаирбекович, Бекболганова Алма Кусаиновна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-01-23″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_31.10.15_10(19)» ebook=»yes» ]

