- Introduction
The aim of this work is to obtain a new factors for T1 by solving Hamiltonian for two levels system and quantum equations. In medical diagnosis using Magnetic Resonance Imaging (MRI), T1 has an important role since the time taken by the patient inside MRI instrument depends on T1. It is therefore essential to know the factors affecting T1, so as to minimize examination time. The classical treatment of T1 shows its dependence of the radio frequency (w) [1 – 6], which is very difficult to change appreciably. So we need to find more factors affecting T1, to minimize T1 and find a new expression for T1.
The interaction of radiation with matter can be represented by the Hamiltonian H, where H equals to:

Where:
H 0 is the free part of the Hamiltonian. H` is the perturbed part of the Hamiltonian.
By solving equation (1.1), (2.1), (2.2), (2.3) we obtain that
T1 is proportional to 1 / w

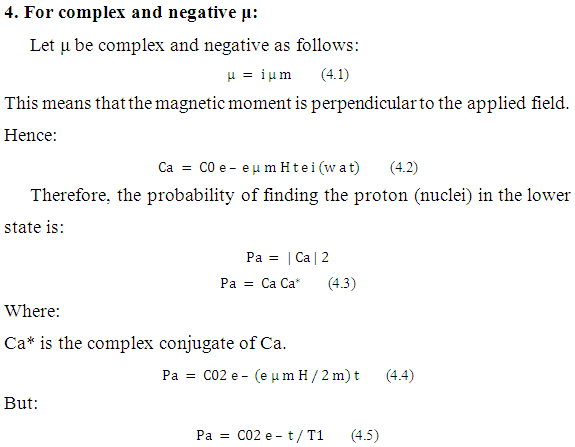
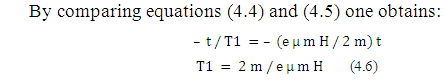
From equation (4.6) one deduces that the relaxation time T1 depends on the mass and that also the relaxation time T1 is in inverse proportion with the susceptibility and with the applied field H.
When the mass m is large, T1 is very long. This is not surprising since when the nuclei are heavy, they move very slowly to restore their maximum value.
Also T1 is short when the susceptibility is large. And this also agrees with our common sense because when the susceptibility is large, the proton responds very quickly to the applied field and it returns in a very short time to the original value. The same holds for H.
- Strong magnetic field and frequency:
For a very high photon frequency (wp) and very strong magnetic field (H) can be get the following equation:



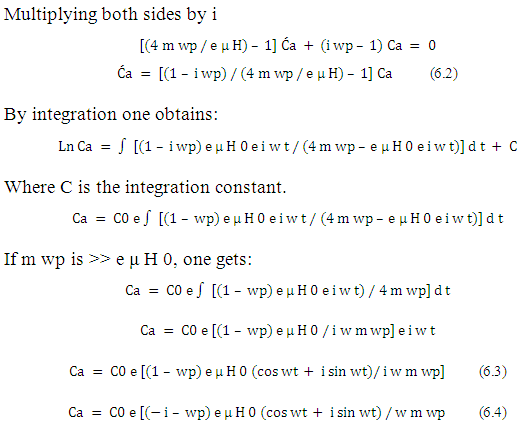

- Conclusion:
A general solution is obtained to find the longitudinal relaxation time T1. Classical solutions are obtained as shown by equations (107),(91),(92).
A relation between T1, the mass m ,the magnetic field H and the susceptibility (μ χ )is also obtained in equations (128),(134),(142),and(152) it is found that :-
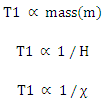
These relations are in complete conformity with our common sense because a large mass particle needs a very long time to respond to the applied field while high susceptibility material responds very quickly to the external field. This indicates that the quantum treatment is more promising than the classical one .This is because, beside classical solutions obtained by quantum approach, additional solutions solutions showing the dependence of on m, H, and χ is also obtained.
References
- Feynman, R. P. &. Hipps, A. R. Quantum Mechanics and Path Integral. Mc Grow Hill New York, 1965.
- Mathews,P. T. Introduction to Quantum Mechanics’, 3erd. Ed., London, 1974.
- Schiff, L. I. Quantum Mechanics, 3rd. Ed., Japan, 1984.
- Meier, F.& Zakharchenya, B. Optical Orientation. Amsterdam, 1984.
- Bray, A. J. & Mc Kane, A. J. Phys. Rev.Lett.62, 493. 1989.
- Mc Kane, A. J. Phys. Rev. A 40, p 4050. 1989.
- Maialle, M. Z. Phys. Rev. B 47, p15776.1993.
- Smith, J. R. & Zangwill, A. Phys. Rev. Lett. 76, 2097.1996.
- Amad, T. Phys. Rev. Lett. 78, 1355. 1997.
- Kogan, S. Phys. Rev. Lett. 81, 2986.1998.
- Schaum series, ‘Vector Analysis’, 4th Ed. Egypt 1998.
- Lmamoglu , A. Phys. Rev. Lett.83, 4204.1999.
- Barkard., G. Phys. Rev. B 59, 2070. 1999.
- Zaliznyak , I. A. Phys. Rev. Lett.83, 5370. 1999.[schema type=»book» name=»Determination new factors for Longitudinal Relaxation Time T1″ description=»In this work, new factors for Longitudinal Relaxation Time T1 obtained by semi classical treatment where atoms treated quantum mechanically and radiation treated classically. The treatment shows that the longitudinal relaxation time (T1) depends on the mass, magnetic permittivity, applied magnetic field and frequency.» author=»Hamad, Kamal Ali» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-02-07″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_29.08.15_08(17)» ebook=»yes» ]

