Vehicular traffic flow and related problems have attracted much attention among physicists in recent years1‘2 and a number of cellular automaton (CA) models3—9 have been proposed. These CA models have the advantages of being simple and easily implemented for numerical simulations, while capturing the essential features in realistic traffic flow.
They also provide some simple examples of a class of problems in driven diffusive systems. The Nagel-Schreckenberg model (NaSc model)3‘ is one. of the most-studied CA models in which the cars are allowed to accelerate, if permitted by the spacing in front, gradually up to a-maximum speed vmax, while taking into consideration a probabilistic delay modelling of the driver’s behavior. The model shows interesting features in the average speed as a function of car density.1 modified , these ear-based models Suitably can be turned into agent-based models for the interesting area of modelling pedestrian behavior.10‘
In complex adaptive systems,11‘ agents (drivers) are provided with global information based on which they make decisions. In traffic flow problems, drivers traveling from point A to point B prefer to take the route with the minimum travel time. The travel time of a route, in turn, depends on the number of drivers taking that route. Common ways of transmitting updated global information to drivers include electronic messages displayed on the road, radio broadcasting, and online images of traffic flow on major roads distributed through the internet. While most traffic flow models do not consider the decision making of drivers based on global information, Wahle et a.,12 recently studied a CA model in which a percentage of drivers (referred to as dynamic drivers) decide to take one of two possible routes of equal length from point A to point B. The dynamics within both routes follows the NaSc model. The global information provided is the latest transit time of the two routes, i.e., the time taken by the most recent car at the exit to travel the entire route for both route .4 and route B. Wahle et a.,12 reported detailed numerical simulation results for their model and found that the number of cars in each route exhibits oscillatory behavior with high amplitude. This can be understood in that when a route. is announced to be »faster» with a shorter transit time, more drivers at the entrance will decide to take that route until it becomes crowded again. This scenario of drivers trying to enter a route with fewer cars is reminiscent of that in the minority game13-15 in which agents are competing to be in the minority group.
Once a route is entered, the dynamics is governed only by the cars in front. The announcement of the transit time thus leads to a delayed effect in that a shorter transit time for the car at the exit does not reflect the actual traffic flow inside the route. In the present work, we report the results of numerical simulation on a modified model in which the global information is the instantaneous average speed of cars in the routes. This is more realistic in that many modern cities are now equipped with such smart traffic systems with remote video cameras installed along major roads. Videos of real-time traffic flow, reflecting the speed of cars on the road, are broadcast online through the internet. Radio and television stations also make use of such information in broadcasting. Our numerical results reveal that while the oscillatory behavior in the number of cars persists, the amplitude has become much lower. The result represents a better spread of the vehicles into the two routes and thus results in a higher traffic flux.
For simplicity, we study a two-route CA model as in ref. 12. In every time step, there is one vehicle trying to enter the system. At the modified, entrance, each driver has a choice of getting on route A or route B. The routes are of equal length L. Each route is a single lane subdivided Each cell can be either empty or occupied by at most one vehicle at a given instant of time. The speed of each vehicle is given by v € {0,1,…, vmax}> where vmax is the maximum speeci allowed on the road. Once a route is entered, the motion of the cars follows the NaSc CA mode.31 The rules for updating the position x of a car are as follows, (i) Acceleration: v — min(v+1, vmax) giving a gradual increase in speed, (ii)’Deceleration: v = min(v,gap) so as to avoid collisions, where the gap is the spacing in front of a car. (iii) Random Delay: with a certain probability p that v = max (v/ — 1.0). (iv) Movement: x = x + v, which give’s the position of the car in the next time step.
The decision-making process based on global information is introduced as follows. In every time step, we announce the instantaneous average speed on the road, which is given by the average displacement per car in the most, recent time step. This information is made available to all drivers. As in ref. 12, we consider two different types of drivers, namely, static and dynamic drivers. The static drivers are those who ignore the global information and select the route according to their own preference. We model them as having a probability q of selecting route A and probability (1 — q) of selecting route B. The dynamic drivers are those who always make use of the global information. They always choose to enter the route with the higher-instantaneous average speed. Note that if a vehicle is not able to enter the chosen route due to car blockage at the entrance, the car is simply deleted and no new car enters the system in that turn. At the exits, one car may leave each route in each time step after traveling through the route.
We have carried out detailed numerical simulations using our model. Unless specified otherwise, the parameters are chosen to be L = 2000 for the length of the routes, p = 0.25 for the probability of delay, and vmax = 3 cells/time step for the maximum speed. In each run, 2 x 10 time steps are carried out. The system typically reaches the steady state after 80,000 time steps.
First, we study the case of q = 0.5, i.e., when the static drivers randomly select a route at the entrance. This is the case discussed in ref. 12 and we will compare the results of the two models to study which piece of global information, travel time or instantaneous average speed, is more effective in terms of road usage and user’s travel time. Let Sdyn be the fraction of dynamic drivers. Figure 1 shows typical results for the travel time and number of vehicles in each of the two routes for Sdyn = 0.5 and q — 0.5 in a time window after the steady state has been reached. The number of vehicles oscillates slightly with time as a result of the decision-making process. In Fig. 1, the results corresponding to the model in which the transit time is announced are included for comparison.
Announcing the average speed on the road suppresses the amplitude of the oscillation in the number of cars and thus the roads are more effectively used. The mean number of cars on each route is about 271 in the present model, while it takes on the value of 240 when the transit time is announced. The lower mean number of cars when
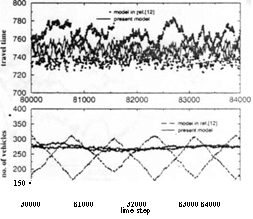
Fig. I. The number of vehicles (lower panel,1 .uul the travel time (upper panel! as a (unction of time .in a time window after the steady state ha.s been reached. The parameters are .s,lv„ = 0.5. r, = :j. ami p = 0.25. Results for the model in which the transit time is announced (ref. 12) are included for comparison.
the transit time is announced is a result of the longer period of time during which a route has a smaller number of cars than in the present model-Qualitatively, this result in turn is a result of the delay effect in the model in ref. 12. When the announced transit time for a route becomes shorter, dynamic drivers consistently try to enter that route. This leads to congestion near the entrance and results in a possible blockage of cars entering the route. Once this congestion starts to develop, it takes a long time, namely, the time for the newly entered cars to travel to the exit, to report a transit time that actually reflects the congestion. Thus the blockage would last for a
on a route as compared with the present model. Announcing the average speed has the effect of spreading the cars more evenly onto the routes and suppressing the blockage at the entrance. The upper panel in Fig. 1 shows the time of travel along both routes over the same time window. Due to the delay effect in the model of ref. 12, the transit time oscillates with a higher amplitude in both routes, while in the present model, the transit time oscillates only slightly with a much lower amplitude. The mean transit time for both models is about 749 time steps, because in both cases, the car density in each of the two routes is low and hence the transit time is mainly governed by the random delay in the NaSc model.
The figure of merit in traffic flow is the flux, which is obtained as the product of the density and the speed. The total flux on both routes, averaged over a time window, is shown in Fig. 2 as a function of the fraction Sdyn of dynamic drivers for q = 0.5 for the two sets of global information. As Sdyn increases, the flux for the case in which announcing the transit time is announced decreases substantially while the flux of the present model changes only slightly. Our results thus show that announcing the instantaneous average speed is more efficient in terms of road utility. It is interesting to note that for q = 0.5, the introduction of dynamic drivers into
the system reduces the flux. This is because the car density in each route is actually in the low-density regime of the NaSc model. We can estimate the number of cars and car density as follows. In the low-density regime. ‘» the average speed in each route is given by v = vmax – p= 2.75 cells per time step. The probability that a car can enter the system is 0.75.17 The average number of cars in the two-route system is then about 0.75L/v 545 for the chosen parameters. Each route thus carries about 272 cars on average, a number vvhich is consistent with our numerical results shown in Fig. 1. The car density in each route is thus around 0.136 cars/ cell, which is consistent with our assumption that the density is low. In the low-density regime, the speed of individual cars is either 2 or 3 for vmax = 3, depending on random delay. In this case, the flux is more sensitive to the car density. Random selection of routes by all drivers, i.e., sdyn = 0 and q = 0.5, represents a uniform distribution of cars into the two routes and results in a slightly higher density in each route. We also note that the instantaneous average speed gives information averaged over the whole route, while jamming of cars occurs more frequently at the entrance to the routes.
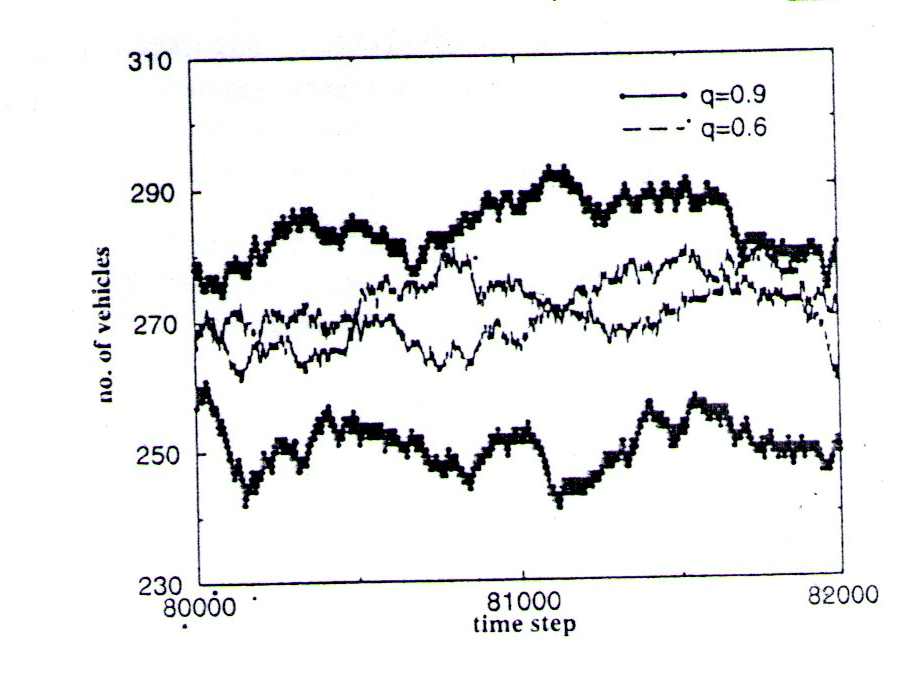
The number of vebicles as afuntion of time in a time window after the steady state has been reahed result for two different value of q,q=0.6 &0.9 with sdyn = 0.5 are shown .
Next, we study the effects of different values of q for the static drivers. Very often, drivers do not select a route randomly. Instead, they may have a preferred route and thus q≠ 0.5. Since the two routes are identical, it is sufficient to study cases with q > 0.5. Figure 3 shows the number of vehicles in the two routes for the cases corresponding to q = 0.6 and 0.9, with sdyn taken to be 0.5. We note that the vehicle density in the •two routes becomes increasingly asymmetric as q increases,, although the densities are still in the low-density regime. Given that the static drivers tend to crowd onto a particular route, the introduction of dynamic drivers can now improve the performance of the two-route system. In Fig. 4, we show the flux as a function of sdyn for different values of q both for the present model (symbols) and the model in ref. 12 (lines). In the present model, the flux for finite sdyn is now higher than that of Sdyn — 0, indicating a better performance. The global information provided to the dynamic drivers
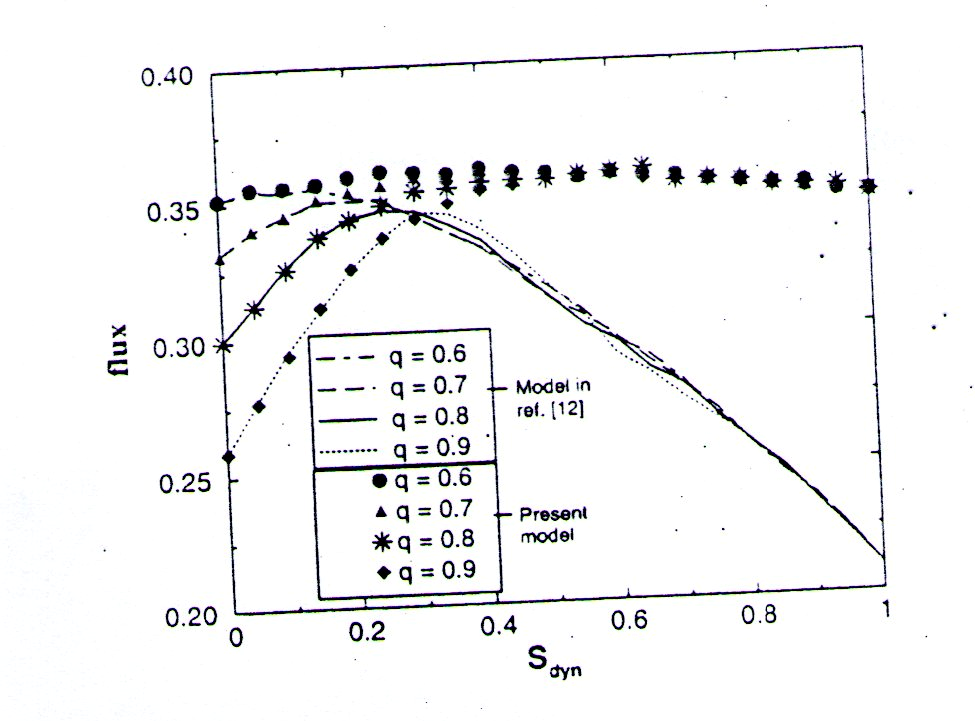
Fig. 4. The flux as a function of the fraction of dynamic cars s.i, for q = 0.6; 0.7. 0.8, 0.0. The symbols represent results of the present model and the lines are results of the model in winch the transit time is announced (ref. 12).
becomes useful. The flux is more sensitive to .sdya and q for Sdyn < 0.5. For sdyn > 0.5, the flux is only weakly dependent on sdyn and q, as there are fewer static drivers r to form the crowd in one route. The flux exhibits a peak for intermediate fraction of dynamic drivers around 1 Sdyn = 0.5. Note that a small fraction of sdyn leads to an increasing flux in both models since the behaviour is dominated by the many static drivers. When transit time is announced, however, the flux decreases with , increasing stdyn for higher values of 5ayn. For sdyn > 0.3. : the flux in the present model is higher than the flux in the model in ref. 12 for all values of q.
In summary, we proposed and numerically studied a two-route traffic model with a built-in decision-making process. Two types of drivers were considered. The instantaneous average speed was provided to the dynamic drivers for making decisions. It is shown that announcing the instantaneous average speed on the routes as global information results in a better performance in terms of the traffic flux rather than announcing the transit time. When the static drivers randomly select a route, the introduction of dynamic drivers does not
Letters
improve the traffic flux of the system. However, when the static drivers tend to select a particular route, the presence of dynamic drivers gives a higher flux. We note that both the present model and the one in ref. 12 give low car densities along the routes, the values of which are governed by the way in which cars are introduced into the system at each time step. It is thus expected that the flux will be more sensitive to the global information if alternative ways of introducing cars, leading to higher car density in each of the routes, are used.
- chowdhury. L santen & A. schadshneider: phys. Rep 329 (2000) 199.
- Helbing: Traffic and related self-driven many-particle system a review available as cond-mat/0012229.
- Nagel and M. Schreckenberg: J. Phys. I (France) 2 (1992) 2221.
- Fukui and Y. Ishibashi: J. Phys. Soc. Jpn. 65 (1996) 1868.
- Nagatam: Phys. Rev. E 48 (1993) 3290.
- H. Wang, Y. R. Kwong and P. M. Hui: Phys. Rev. E 57 (1998) 2568.
- H. Wang, L. Wang. P. M. Hui and B. Hu: Phys. Rev. 6, 58 (1998) 2876.
- (). Biham. A. A. Middlcton and D. Levine: Phys. Rev. A 46 (1992) R6124.
- H. Chung. P. M. Hui and G. Q. Gu: Phys. Rev E 51 ! 1995) 772
- Helbing, I. Farkas and T. Vicsek: Nature 407 (2000) 487.
- H. Holland: Emergence: From Chaos to Order (Addison-Wesley. Reading,.MA, 1998).
- Wahle, A. L. C. Bazzan. F. Kiugl and M. Schreckenberg: Physica A 287 (2000) 669.
- Challet and Y. C. Zhang: Physica A 246 .1997) 407.
- F. Johnson. M. Hart and P. M. Hu:: Physica A 269 (1999) 1.
- Hart. P. .leffcries. P. M. Hui and N. F. Johnson: Eur. Phys. J. B 20 (2001) 547.
- W. Huang and C. W. Tsai: Phys. Rev. E 63 (2001) 0120101.
- Cheybani. J. Kertesz and M. Schreckenberg: Phys. Rev. E 63 (2001) 016108.[schema type=»book» name=»A TWO – ROUTE TRAFFIC FLOW MODEL EFFECTS OF ANNOUNCING GLOBAL INFORMATION» description=»It is shown that announcing the instant taneons average speed on the routes results in abetter per formance of the two – route system in terms of the traffic flux compored to announcing the transit time. Atwo –rout moded with abuit- in decision making process is proposed & studied anumerically. The instantnneous average speeds on the routed are announced as global information. Two types of drives, dynamic & static, are introduced. The dyroamic drivers use the global information for moking decisions. When the static drivers randomly select aroute. The presence of the dynamic driver dose not improve the traffic flux of the static drivers tend to select aporticular route, the peresence of system. When the dynamic divers lead to ahigher flux. Our model thus incorporated the effects adaptability into the celluar automation modets of traffic flow . » author=»Dr.Abdul Salaam .W.Alkhazraji» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-02-01″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_26.09.15_10(18)» ebook=»yes» ]

